Five percent of the marbles in a jar are black.
One fourth of the marbles are green.
One half of the marbles are yellow.
The rest are white.
If there are 16 white marbles, how many marbles are in the jar?
Five percent of the marbles in a jar are black.
One fourth of the marbles are green.
One half of the marbles are yellow.
The rest are white.
If there are 16 white marbles, how many marbles are in the jar?
A bag contains 6 green, 5 gray, and 4 violet disks.
If 2 disks are drawn at random from the bag, what is the probability that the disks drawn are green?
If two dice are rolled 72 times, how many times is the sum of the two top numbers expected to be 12?
A city hall contains 165 chairs. The first row has 10 chairs.
Each additional row has one more chair than the row before it.
How many rows are there?
Which number could be removed from the set without changing the average (arithmetic mean of all the numbers)?
The first person is 100 cm tall.
Each next person is 20% taller than the person before.
Who will be taller than 2 meters first?
Five students put their sandwiches into five paper bags.
The bags are randomly distributed to the students.
What is the probability that exactly 4 students receive the correct bag?
Four kinds of apples are combined in a box.
I select apples from the box without looking.
How many apples must I draw to be sure of getting at least three of one kind?
Statistics show that for every 100 babies born in Funny Town, there are 10 more boys than girls.
What is the probability that Mr. Smith's newborn twins are boys?
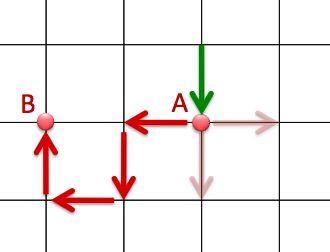John arrives at crossroads A from the North.
He makes four moves each time randomly choosing one of three directions.
For example, he could end up at point B.
What is the probability that he finds himself back at point A?
99 numbers have an average of 101.
Ninety of these numbers have an average of 100.
What is the average of the other nine numbers?
The average of a set of 12 numbers is 1.
If 18, 50 and -20 are added to the set, what is the new average?
Anna has a bag with 90 wafers.
She eats 14 wafers on the first day.
Every day, she eats one wafer less than the day before.
In how many days does she eat all the wafers?
Bobby takes five tiles with the letters of his name and places them into a bag.
He randomly picks one tile after another from the bag, and does not replace them in the bag.
What is the probability that he chooses the tiles in the same order as his name?
Six standard dice are rolled and the numbers on the top faces are added together.
What sum is the most probable?
Two princes and two princesses are ready to marry.
Everybody independently chooses a partner without telling anyone.
What is the probability that at least one princess chooses a prince that chooses her?
Assuming that boys choose girls and girls choose boys.
I have eight dimes; five are real, and three are fake.
Whenever a real dime is flipped, it comes up heads with a probability of 0.5.
A fake dime comes up heads up with a probability of 5/6.
What is the probability that a randomly chosen coin will come up heads?
A team of three children, Anna, Bill and Cindy, independently answers true-or-false questions.
Anna answers 90% of the questions correctly.
Bill and Cindy answer 50% of the questions correctly.
The answer is accepted as the team's response when the children give the same answer.
If their answers are different, then the result is ignored.
What is the probability that a team response is correct?
Dueling Idiots Problem: three idiots participate in a duel.
They shoot at the same time.
If each idiot randomly chooses one of the other two idiots and successfully shoots him, what is the probability that at least one idiot will survive?
There are 10 girls and 10 boys in a class.
A teacher randomly chooses two students.
What is the probability that they are a boy and a girl?
Two dice are thrown.
You can see all 12 numbers except 2 faces that are on the table.
All the numbers on the ten visible faces are added.
Which sum of the numbers on the faces is the most probable?
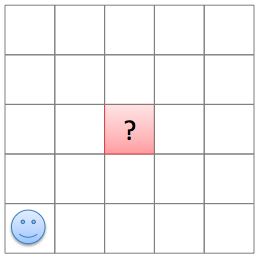A chip is placed at the bottom left corner square of a 5 x 5 grid.
The chip is moved one space upwards or to the right. One of the directions is randomly chosen, for example, by flipping a fair coin.
Find the probability that the chip reaches the center square of the grid in 4 moves.
After a gun is fired in a saloon, 75% of the cowboys have a wounded ear, 80% have a wounded eye, 85% have a wounded arm, and 90% have a wounded leg.
What is the smallest percentage possible of cowboys who have all four wounds?
If we set out by ranks of 10, we will be one short.
We will also be one short if we set out by ranks of 9, 8, 7, 6, 5, 4, 3, and even 2.
Yet there are fewer than 5000 participants.
How many are we?
Source: Marie Berrondom, Mathematical Games, 1983
It takes 2 cards to build 1 floor of a card house.
It takes 7 cards to build 2 floors of a card house.
It takes 15 cards to build 3 floors of a card house.
How many cards does it take to build a 10-story house?
Anna earned an average of 80% on her four exams.
If she never earned more than 90% what is the lowest possible percentage score she could have received in any one of the exams?
John answered 100 4-option multiple-choice questions.
He is sure that he correctly answered 50% of the questions.
In 30% of the questions, he chose the answer among two options, and he answered all other questions by randomly guessing among the four options.
What score does John expect to receive on the exam?
Forty non-zero positive numbers are written in a row.
The average of the first two numbers is 1.
The average of the second and third numbers is 2.
The average of the third and fourth numbers is 3 and so on.
What is the last number in the row?
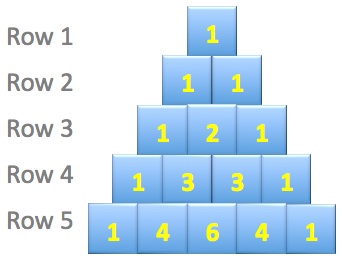This picture shows the first five rows of Pascal's triangle.
What is the sum of the numbers in the 10th row of the triangle?
San Jose Scrabble® Club No. 21 published a three-letter word list that included 1014 English words.
Estimate the percentage of these words compared with all possible three-letter combinations?
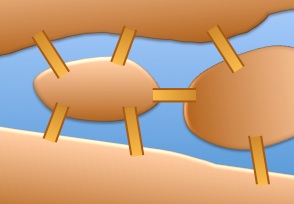In a city, there were seven bridges.
There was a tradition to walk and cross over each of the seven bridges.
If a person starts and finishes at the same point, what is the smallest number of crossings the person would have to make?
An entrepreneur wants to hire the best person for a position.
He makes a decision immediately after the interview.
Once rejected, an applicant cannot be recalled.
He interviews N randomly chosen people out of 100 applicants, rejects them and records the best score S.
After that, he continues to interview others and stops when the person has a score better than S.
What number N do you recommend to the cruel man?
A group of kids with dogs go for a walk.
There are 49 feet and heads altogether.
There are more dogs than kids.
How many dogs are there?
Bob is rolling two dice and will subtract the second number from the first number.
What result is Bob most likely to roll?
The average of twelve numbers is 8 and the average of another set of eight numbers is 12.
What is the average of all these numbers?
Fifteen numbers have an average of 10.
Five of these numbers have an average of 5, four other numbers have an average of 4, three an average of 3, and two an average of 2.
What is the remaining number?
The average (arithmetic mean) of a set of 10 different numbers is 98.
If the numbers 40 and 140 are removed from the set, what is the average of the remaining numbers?
Anna has 3 bags of marbles.
The first contains 5 white marbles and 5 green marbles.
The second contains 2 white marbles and 8 blue marbles.
The third contains 16 white marbles and 4 green marbles.
If she randomly selects a single marble from each bag, what is the probability that all three marbles will be white?
John has an average of 87 on his two math exams.
To earn an A, he must have a 90 average.
What is the lowest grade he must earn on the next exam to raise his average to 90?
Everyone in tenth grade classes voted on a motion.
Sixty percent of the girls voted YES.
Forty percent of the boys voted YES.
The motion passes if over 50% of the votes are YES.
In which class was the motion rejected?
Alex received a 60 on his essay and an 80 on his final.
He got a 90 on class participation.
The essay counts as 30% of his grade.
Class participation counts as 20% of his grade.
What is his grade?
Gerry and Jane are younger than 25.
The probability that two randomly chosen people in their city are younger than 25 is 25%.
What is the probability that 4 randomly chosen people from the city are younger than 25?
Jane and Gerry visit a casino.
In one game, they have a 1/5 probability of winning $100 and 1/2 probability of losing $50.
They have also a chance of no win / no loss.
What is the most likely amount of money they will win (or lose) at the end of 100 games?
Gambling is bad!
John is sick 12 days per year.
The probability of being sick on a Saturday or a Sunday is two times less than on any other day.
What is the probability that John will be sick on a Monday?
Abbey has a dog Abby.
She places 5 tiles with the letters of her surname into a bag.
She picks up one tile after other without looking.
What word has the greatest probability of appearing in the correct order from the beginning?
John sent an email to his three partners.
Everybody answered and copied the answer to all others.
A total of 12 emails were sent.
How many emails are sent if there are 20 people communicating in the same manner?
An average baby is about 20 inches (51 cm) long and weighs approximately 6 to 9 pounds (2700 to 4000 grams).
How many times heavier than a baby is an adult?
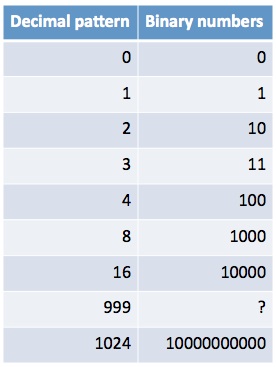The binary numeral system represents numeric values using two symbols: 0 and 1.
How is the number 999 written in binary code?
If 2 salesmen can sell three luxury cars in 4 days, how many luxury cars can five salesmen sell to six clients in 7 days?
If the probability of an accident occurring in 4 years is 0.9999, what is the probability of an accident occurring in 1 year?
Alex(A), Beatrice (B), and Craig (C) work on a project.
(1) Together, A and B can complete it in 10 days.
(2) Together, B and C can complete it in 12 days.
(3) Together, C and A can complete it in 15 days.
If Alex does it alone, how many days will it take?
I ask you to pick a number from 1 to 100.
I then ask you, “Is the number greater than X?”
You must truly answer yes or no until I tell you the number.
What is the maximum number of questions I ask you if I choose the optimal strategy?
Here X is the number of my choice.
Guesstimation
A man can jump up to four times the length of his own body.
Frogs can jump up to fifty times their length.
A flea can jump 350 times the length of its own body.
What is the average length of these three jumps?
Alex must match three different numbers chosen from the integers 1 to 33 in any order to win a lottery.
He bought 333 tickets, each with a unique combination of numbers.
What is the probability of winning?
In the United States, the average life span is 65 years and the average female gives birth to 2.6 children.
The average age when a female bears children is less than 30.
How many descendants would the female have at the end of her life?
After a test of a code, John detected 2 errors and Mary discovered 3 errors in the same code.
There is one error in common.
Estimate the number of errors that are still undetected.
After a 20% discount and 8% tax, a set of tin solders costs $540.
What was the original price of the set?
One bag contains two white marbles, another bag contains two black marbles, and a third bag contains one white marble and one black marble.
I pick a random bag and take out a black marble.
What is the probability that the remaining marble from the same bag is also black?
A school offers the following dinner choices:
First course: soup or small salad;
Main course: vegetarian, chicken, pizza, cheeseburger or fish;
Dessert: apple cake, doughnut, fruit salad, ice cream or milkshake.
How many school dinners will I have eaten before I have to choose a combination that I have already eaten?
The average IQ of 100 students is 101.
If the first ninety-nine students each have an IQ of 100, what is the IQ of the last student?
Anna spent 120 Swiss francs in a Swiss souvenir shop. She was charged an extra 2% for paying with her credit card.
How much did she spend in USD?
Use an exchange rate of $1 = 0.96 Swiss Franc
If the first President of the USA George Washington took office in 1789 and the fortieth President Roland Reagan completed his duty in 2004 what is average duration of the term for the American Presidents?
Javier Sotomayor (Cuba) is the men's record holder with a jump of 2.45 m set in 1993, the longest standing record in the history of the men's high jump.
Javier is 1.95 m tall.
What percentage of his height did he jump?
Data source : Wikipedia
Bob used to weigh 100kg.
His new stressful job causes him to lose 10% every month.
How much does he weigh after 3 months of work?
How many 9s are there in the result of the multiplication:
12345 x 99999 ?
Don't use the calculator.
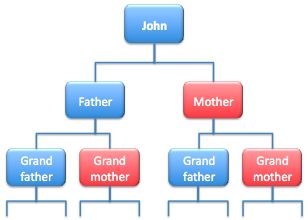John's family tree includes 10 generations.
What is the minimum number of people on his family tree if there were no intermarriages?
A line containing 9 keyboard letters on Gerry's laptop does not work.
If his password consists of 2 letters, 4 numbers, and 1 special symbol, what is the probability that he will be able to log in?
Gerry estimates that two angles of a triangles have a measure between 50 and 70 degrees each.
If this is true, what would be estimate for the third angle?
What is the difference between 11 in decimal (normal) and binary systems?
A binary number is made up of only 0s and 1s.
There are 800 students in a school.
The students' average age is 12 years and 60% of them are girls.
What is the difference between the sums of girls and boys ages?
If you toss a dime five times and it lands heads up three times, what are the chances it will land heads up if you toss it again?
The masses of sugar and water in my 200 g tea cup are in the ratio 1 : 9.
If I drop two 25 g cubes of sugar into the cup, what will be the new percentage of sugar?
(We assume that the cup does not overflow in the process!)
The cost of living increases uniformly by 44% in a period of two years.
What is the annual percent increase?
Gerry and Jane like to look at registration plates of cars that pass by.
They add the three digits and bet on a result.
Among the values below, what is the best sum of three digits to bet on?
If I put these balls in a bag and take two balls without looking, what is the probability that the two balls are white?
I roll two dice, one with the left hand and one with the right.
If the left hand die gives an odd number, the overall score is zero.
If the right hand die gives an even number, I roll it again and again until it is odd.
The score is the sum of the two numbers, except for the previously mentioned case.
There are exactly 6 possible scores: 0, 3, 5, 7, 9, and 11.
What is the probability of a score of 3?
The problem was suggested by Leslie Green
Buy 2 for the price of 3 and get 50% off!
What is the final rebate do you get?
'Buy, buy, says the sign in the shop window; Why, why, says the junk in the yard.' - Paul McCartney
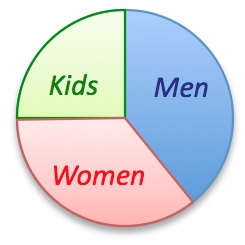The pie chart shows the number of men, women and kids in a county.
What is the ratio of children to women?
Gerry tosses a coin and Jane tosses 2 coins.
What is the probability that Jane has more heads than Gerry does?
Martin has ten thousand dollars in a bank account. The interest rate for his account is 10% every year.
How much money will Martin have in his bank account after three years?
Jane and Gerry compete in a best-of-three match.
If Gerry plays so that his girl-friend has a 60% chance of winning any particular game, what is the likelihood that she will win the match?
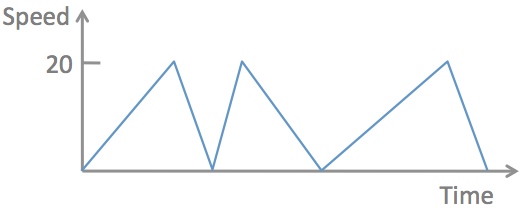Cletus is absolutely, definitely, the worst student the driving school has ever seen. When asked to drive at a steady speed he constantly accelerates too hard, overshoots the target speed, and then brakes too heavily. He has what the instructors call a "heavy foot".
By some miracle he manages to always hit the same top speed of 20 mph before braking in a continuing non-repeating pattern like the one shown.
What is his average speed?
Author: Leslie Green
Leslie Green asks: "In a large village community there are regularly women giving birth to triplets, but surprisingly never twins.
The average number of babies per mother is 1.9
The local nurse visits the next recent mother on her list.
Which is the most probable number of babies she will find?"
Jane has a 5-liter bucket with 5%-fat milk and 3-liter bucket with 3%-fat milk.
What is the fat concentration in the milk if she pours both into a large bucket?
Anton, the highest IQ house ant on the planet, is taking his regular nocturnal walk from one corner of the chess board (1,1) to the diagonally opposite corner (8,8), moving only right or up the board at each successive square. He remembers that on square (5,3) there is a tasty sticky residue, so any valid route must involve this square.
From how many different paths can he choose?
[HINT: You could try an easier problem first.]
Author: Leslie Green
Jake, being bored on a rainy Sunday afternoon, throws a pair of dice 500 times and keeps a record of the results.
What is the ratio of probabilities between throwing one five and all the rest twos, compared to throwing all threes.
Author: Leslie Green
An escaped criminal has stolen a spaceship, and has just instantaneously jumped 1 light year away. On each successive jump she will only be able to jump half the distance of the immediately preceding jump due to heat build-up. Jump engines always take 1 hour to recharge.
My ship can only jump 1/2 light year, but it has a better cooling system so the jump distances drop-off more slowly. My maximum jump distances follow the sequence: 1/2 light year, 1/3 light year, 1/4 light year, and so on.
I can find her with my subspace-tracker. If she is closer than my maximum jump distance I can get close enough to remotely disable her jump-drive and capture her. My jump engines are fully charged.
Can I catch her?
Author: Leslie Green
Despite advice to the contrary from his friends and parents, Timmy has decided on a new strategy to select future girlfriends. He has two “must-see” programs on 5 days of each week. He requires that any future girlfriend must match-up with at least 90% of these programs. Given that there are 20 TV channels available in his area, what is the probability of a match?
Author: Leslie Green
Jane has three parrots.
She said that at least one is a boy.
What is the probability that there is a girl in the trio of parrots?
Lottery 6-digit numbers are from 000001 to 999999. A ticket is considered to have a “special” number if the sum of the first 3 digits is equal to the sum of the last 3 digits.
Find the sum of digits of the largest possible special number.
No digit is used twice in the six digit number.
What is the probability of getting 5 correct answers on A+Click questions in a row if you have no ideas about the correct answers?
One hundred workers complete a project in 100 working days.
Adding any positive number of workers proportionally decreases the team efficiency.
Which number of workers allows a similar project to be completed most quickly?
When three fruits are randomly taken from the box, what is the probability that only apples are left in the box?
Each time a bar of soap is used, its volume decreases by 10%.
How many times would I wash my hands with the piece of soap so that less than one-half its volume remains?
A bag contains six green, five gray, and four violet disks.
How many green disks must be added to the bag so that 75 percent of the disks are green?
The US frequently used banknotes are $1, $5, $20, $50, and $100.
Gerry has 4 of each of these banknotes in his wallet.
He enjoyed the dinner with his girl-friend Jane and decided to pay the $200 total cost himself.
In how many different ways can he pay $200 using his banknotes?
Gerry's rich uncle gave him $2 on his first birthday. On each birthday after that he doubled his previous gift.
What was the total amount that his uncle had given him after the tenth birthday?
Jasmine has just been learning about the binary number system at school. On her way home she wondered how far she could count using just the four fingers on one hand, if a curled finger represented a binary 0 and an outstretched finger represented a binary 1.
To be clear, she was thinking about counting up from zero in whole numbers. How far could she get?
Author: Leslie Green
Kitty has one million marbles, which are numbered from 1 to 1,000,000. Marbles with equal digit sums have the same color and marbles with different sums have different colors.
How many different colors of marbles does Kitty have?
Five students randomly choose their places on a bench.
What are the chances that Gerry and Jane sit together?
The average of 9 numbers is 9. If a number is added to the set, then the new average becomes 10.
What is the value of the number?
Split the number below into 3 parts such that their sum is at a minimum.
(In other words, make 3 groups of the digits without changing their ordering.)
What is last digit of the sum?
8912673450
There are four sisters. If we leave out any one, the average age of the remaining three sisters will be 6, 8, 9 or 10.
What is the average age of all four sisters?
Kitty has 2017 marbles. The marbles are numbered from 1 to 2017. Marbles with equal digit sums have the same color.
How many different colors of marbles does Kitty have?
The maximum capacity of a standard school bus is 72 passengers.
Estimate the weight of people in the bus if a bunch of fathers take the bus to visit their children.
Wikipedia says that the average weight of a male American is 195 pounds or 88.5 kg.
1 tonne = 1,000 kg
You have four different coins about the same size.
You have only a balance to compare the weights of two coins.
What is the smallest number of weighing steps needed to sort the coins from the lightest coin to the heaviest coin?
In factories where food items are packaged, one clever technique for optimally filling bags is to fill 12 nominally equal hoppers with the food, then computer select the 4 which give the closest fit to the required weight. This is better than taking food items such as crisps and putting tiny broken pieces in to make up the required weight. It is also cheaper for the manufacturer to not greatly exceed the minimum weight, and effectively get paid less for each gram of food as a result.
How many combinations does the computer have to check to get the optimal selection?
Author: Leslie Green
A hospital runs a queuing system for non-urgent surgical procedures. This queue always has 100 patients in it and one patient is operated on each day (7 days a week). If a patient is not available on the day of surgery they lose their place to a brand new patient who would otherwise have gone elsewhere. (This is easier than rescheduling 100 appointments.)
Roughly 5% of patients are not available or do not show up for their procedures.
What is the average waiting time reported to the managers of the hospital?
(If a patient does not receive surgery their waiting times are not included in any statistics.)
Author: Leslie Green
The Funny Pins bowling club consists of ten married couples.
The club has decided to create a mixed (man-woman) team for the next tournament by randomly selecting partners. They don't want spouses to play in the team.
How many different teams are possible?
John proudly works for a Secret Service earning $5,000 per week. By mistake his wage was reduced by 10% last week. To fix the mistake, his reduced wage is increased by 11% this week.
Who wins from the changes?
There are a few more than one thousand students in a school.
If 48% of the students are girls, how many more boys than girls are there in the school?
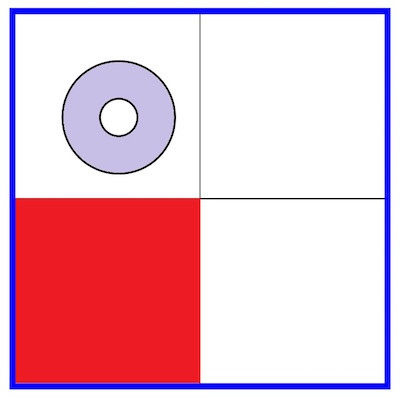The blue square is the plan view of an open-topped box with slippery walls. The washer, which is not shown to scale, is thrown into the box at random, and the washer always lands flat on the bottom. The length of the inside edges of the box is 12 inches. The washer’s outer diameter is 1 inch and its inner diameter is 7/16 of an inch.
What is the probability that the washer lands entirely within the bottom left-hand square (red)?
Author: Leslie Green
There is a simple repeating sequence of numbers:
1, 2, 7, 11, 12, 17, 21, 22, 27, 31, 32, 37, …
This pattern continues up to 1000.
How many numbers are there in the sequence?
Author: Leslie Green
A country boy takes 2 identical ropes, mixes the ends, and asks his girl-friend to tie two pairs of knots on the top.
There is a superstitious tradition in their village that if the result is a ring, then their common life will be long and happy.
According to this tradition, what is the probability of them getting a long and happy life?
The St. Petersburg paradox was solved by Daniel Bernoulli in 1738.
A casino staff member tosses a coin repeatedly until it comes up heads. If heads appears on the first throw, the casino pays you $2. If it appears on the second throw, you receive $4; if on the third, you receive $8 and so on, doubling each time.
How much would the casino be willing to accept from you to consider the game favorable for it?
Three online meteorology (weather forecasting) services have a tendency to make mistakes 1/3 of the time.
They all say that it will rain in the old Swiss town of Murten tomorrow.
What are chances that it really rains tomorrow?
A telephone is locked by a combination of five digits.
Each of the five combinations 15321, 18622, 79643, 73737, and 15597 contains exactly two digits in the right position.
What is the sum of the digits of the combination that unlocks the telephone?
This year Samantha has become very fussy about her birthday present. A square box must be wrapped in blue paper. A round box must be wrapped in red paper. An irregular box must be wrapped in green paper.
The probability of her getting a round box is 50%. The probability of her getting a green box is 1/4.
What is the probability that this spoilt child receives a blue present?
Author: Leslie Green
There is a 0.0001% chance of winning the Jackpot in a lottery that immediately gives the result.
People lined up in front of a kiosk and nine people before Gerry in the line failed to get the Jackpot.
What's the chance of Gerry winning the Jackpot?
In a scene from a film, the baddy is sharing the ill gotten gains with his (comically stupid) henchman by dividing the gold pieces into two 'equal' piles.
'That’s one for you, and that’s one for me'.
'That’s two for you (puts an additional one on the henchman’s pile), and two for me (puts an additional two on his own pile)'.
'That’s three for you (adds one to the henchman’s pile), and three for me (puts three more on his own pile)'.
The final round is 'N for you, and N for me'.
How many times more pieces of gold does the baddy get?
Leslie Green suggested the problem for Aplusclick project. This theme has been repeated at least once. An early version was with Bugs Bunny, 'Racketeer Rabbit' (1946).
There are 110 coins in a pile, 77 heads up, 33 tails up.
I randomly choose 33 coins from the pile and put them in pile A, and I call the remaining coins pile B.
I flip all coins in pile A.
Where is the number of tails greater?
Four nearly identical balls are numbered 1 to 4 and then placed in a bag. The bag is shaken so the balls are mixed up. Jane draws two of the balls from the bag. Jane wins if the sum of the numbers on the chosen balls is greater than the sum of the balls left in the bag.
What is the probability that Jane wins the game?
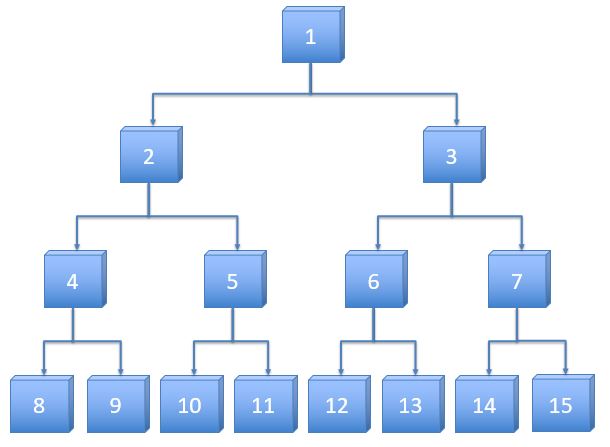The tree pattern has four rows.
If the pattern continues, what is rightmost number in the tenth row?
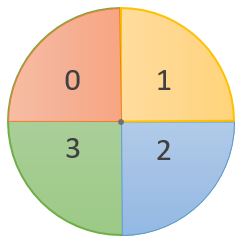Gerry aims at the center (centre) of the large target. He is sufficiently accurate that he always hits the target. He throws 2 darts and adds up the scores.
What is his chance to score 3 in total?
Sammy the Squirrel hides acorns in groups of 3, 4, or 5 per stash, the actual number being pretty random. He creates 200 such stashes in the autumn. When winter comes he only manages to find 5% of his stashes.
On average, how many acorns does he find from his stashes?
Author: Leslie Green
The largest known prime number was discovered by a computer laboratory of the University of Central Missouri in 2016.
257,885,161 – 1
Estimate the number of digits in the number.
Note: log10(2) ≈ 0.3
6 numbers are required to have an average of 9999. The first five numbers are: 9999, 9998, 9997, 9996, and 9995.
What must the last number be to meet the requirement?
Hint:Look for a sneaky method, rather than doing long-addition or algebra.
Author: Leslie Green
Leslie Green asks:
I have an unbiased coin, a fair six-sided die, and an ordinary pack of 52 playing cards. I toss the coin, roll the die, and pick a card at random.
What is the chance that I don't get a head, roll a number less than 5, and don't get a heart?
If the number of women in a company was increased by 50%, and the number of men was decreased by 50%, how did the ratio of women to men change in the company?
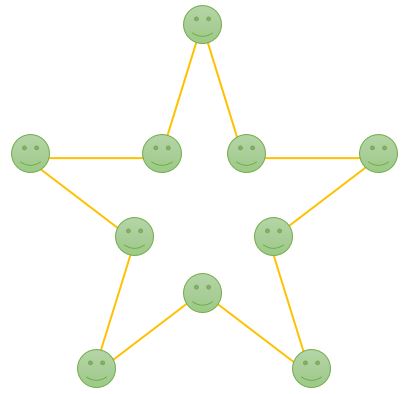Ten brave men are in the corners of a pathway that has the shape of a regular star.
At the same moment in time, each of them randomly chooses a direction and starts walking.
What is the probability that nobody meets another man?
Twenty children dance in a circle.
Everybody has a handkerchief, that he/she gives either to the left neighbor or to the right neighbor.
The choice is random.
What is the expected number of kids with at least one handkerchief?
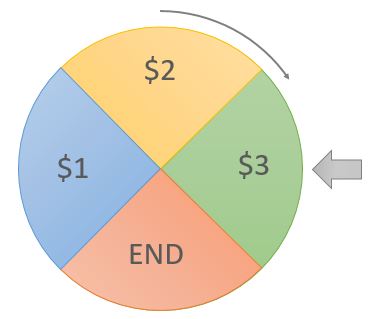You spin a wheel and it randomly lands on $1, $2, $3, or END. If you land on $1, $2, or $3 you get that money and spin the wheel again. You keep receiving money until you land on END.
How much do you expect to win on average?
I keep drawing randomly 1-cent and 2-cent coins until I reach or exceed 1 Euro. The first coin is equally likely to be 1 or 2 cents.
What is the probability that the last coin is 1-cent?
Each of the five keys fits exactly one of five locks.
Imagine the worst scenario: how many times do you test a key in a lock in order to match up all the keys and locks?
The cipher-text shown would be very difficult to decipher by hand if it were not for one crucial mistake. The sender has addressed the recipient by name, and we have guessed that the message is for Betty.
What is the message about?
by Leslie Green
In Timmy's school there are lots of girls of a similar age to him. He estimates that about half are natural blondes and half are brunettes. There don't seem to be any black haired or ginger haired girls for some reason. He has been told that there are roughly as many girls with blue eyes as there are with brown eyes, and other eye colours are also not present.
Estimate the probability that if he picks a girl from his school at random she will be a natural blonde with brown eyes.
by Leslie Green
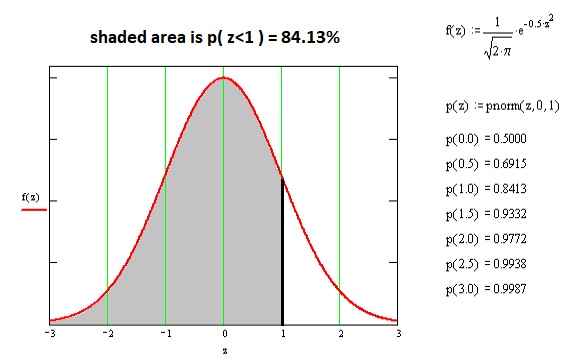We have been told that the local population of men have an average height of 66 inches, and that their height has a standard deviation of 2 inches.
Estimate what proportion of these men have a height in excess of 63 inches.
by Leslie Green
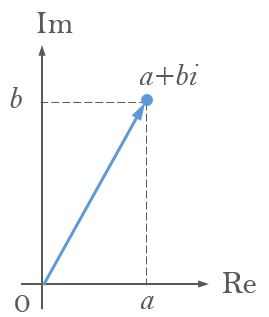Leslie Green asks:
In the field of complex numbers we have a number which consists of a real part and an imaginary part.
The imaginary part is some multiple of i, where i is the square root of minus one.
Given Z = 4 + 3i
and W = -3 - 2i
What is the real part of the product of Z and W?
What is the fewest number of people that could have visited a movie show in the open-air cinema, if exactly 0.8% of the people did not watch the film until the end?
What is the value, written in base 7, of the sum of the two numbers written in base 3 and 6?
123 + 456 = ??7
The probability of a man hitting a target is 1/3.
If he throws 3 times, what is the probability that he hits the target at least once?
This is a single sequence where there is a mathematical rule to go from one position to the next. There are no alphabets involved, this is a purely numerical problem.
1, 8, 4, 0, 7, 3, 10, ...
How many more steps before the 10 is repeated?
by Leslie Green
Gerry throws two dice.
What is the probability that the product of two numbers is even (evenly divisible by 2)?
John randomly chooses a piece of paper from a collection of green, yellow, blue, violet, and rose sheets. There is an equal probability of choosing any particular color.
At exactly the same time, Jane randomly chooses a pen from a collection of green, yellow, blue, violet, and rose pens. There is an equal probability of choosing any particular color.
Neither John nor Jane know what the other has selected.
Jennifer takes the pen and paper and writes a note.
What is the probability that the writing will be visible, given that writing using a pen of the same color as the paper will not be visible?
by Leslie Green
How many small circles are inside all three squares?
The sum of N consecutive integer numbers is 2090. 
What is the average of the smaller of two random numbers from 0 to 1?
If you are a redhead you have more than the average amount of hair. 
Which year has had the greatest number of Roman numerals in it?
Every day, a stock price of $444 is either increased or decreased by 4%. 
What is the probability of getting blue?
What time is it 1234 minutes after 1:23 a.m.?
What is the sum of the first 13 numbers that are evenly divisible by 13?
Which of the following is closest to 
Find X.
What is the simple interest earned on an account of $800 at annual 8% interest for 9 months?
What percent of 120 is 150? 
Express nine using two zeros and two ones: