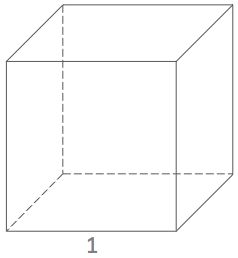
A hall is cube-shaped.
The volume of the hall is 216 cubic meters.
The door is 3 meters high.
Find the length of a side of the floor.
A hall is cube-shaped.
The volume of the hall is 216 cubic meters.
The door is 3 meters high.
Find the length of a side of the floor.
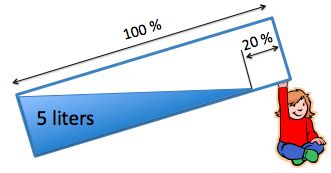The aquarium was full of water.
A girl has tipped it on its side,
so five liters are left.
How much water does the aquarium hold when it is full of water.
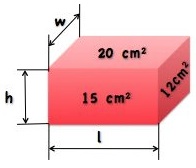One face of a rectangular box has an area of 15 square cm. Another face is 20 square cm and the other face is 12 square cm.
What is the height, h, of the box?
This large cube is made from smaller wooden cubes.
All of the faces of the large cube are painted blue, and then it is taken apart.
What fraction of the surface is blue?
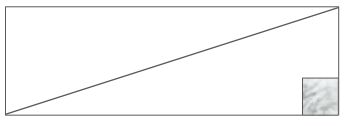A rectangular floor measures 3 meters by 9 meters.
It is tiled with one-square meter tiles.
Through how many tiles would the diagonal line in this rectangle pass?
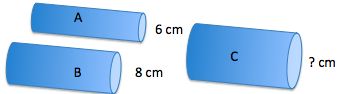A sports club is replacing its water supply lines for a swimming pool. The current system uses two pipes, A and B, which have circular cross-sections with diameters of 6 and 8 cm, respectively. The club decides to use a single replacement pipe with the same capacity.
What is the diameter of the new pipe?
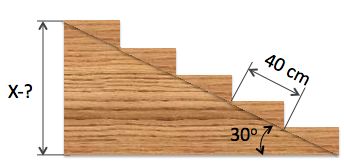John is building a flight of stairs.
Each stair is the same size.
What is the height of the flight of stairs X?
Members of the Green Tennis Club are creating a logo.
The logo of the club is a blue square with a green shape inside.
What percentage of the logo is blue?
Mr. Clever gave his students this pattern of gray tiles.
Develop an equation to represent the number of gray tiles, t, for any size of the inner square, n.
A wheel with a red mark on it is rolled along a straight line.
What is the path the mark follows during one revolution?
The figure consists of congruent squares.
The perimeter of the figure is 10 meters.
What is the area of the figure?
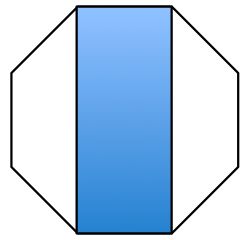The figure shows a regular octagon.
What is the area of the colored part as a fraction of the area of the entire octagon?
I want to build a fence around a rectangular garden.
The garden has an area of 100 square meters.
The fence posts must be placed 1 meter apart.
What is the minimum and maximum number of fence posts needed?
The bigger star is similar to the smaller one.
It is twice the height of the smaller star.
How much greater is its area?
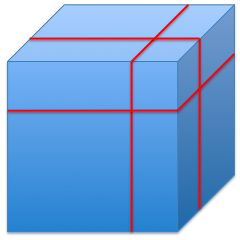Cut 1 cube into 8 pieces. One of the pieces is a cube whose volume is three times less than that of the original cube.
What is the percentage of new surface area compared with the original cube's surface area?
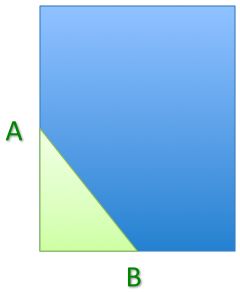
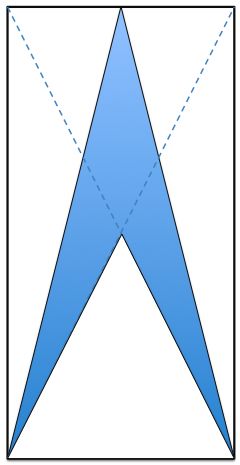The arrow top is at the midpoint of the edge of the rectangle.
What fraction of the rectangle is shaded?
Each diagonal of a cube is increased by 50%.
What was the percentage increase of the volume of the cube?
A and B are midpoints of the corresponding sides of the rectangle.
What fraction of the rectangle is the green part?
John cuts a large piece of cheese into small pieces using straight cuts from a very sharp cheese wire.
He does not move the pieces from the original shape while he cuts the cheese.
How many rectangular pieces of cheese can he get using only five cuts?
All triangles are inscribed in circles with a diameter of 1 meter.
Find the triangle with the largest area.
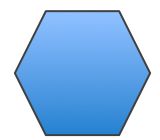Two polygons are congruent if their corresponding sides are equal in length and their corresponding angles are equal in size.
In how many ways can a regular hexagon be divided by a straight line into two congruent pentagons?
Fifteen billiard balls perfectly fit into a triangular rack.
What is the largest number of the balls that fit into the rack when its side lengths are increased by 20%?
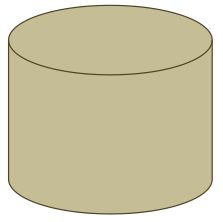I want to cut round bread into eight equal pieces.
What is the smallest number of straight cuts I can make to achieve this?
The diagram shows my square pond with a tree in each corner.
How much can I increase its area if I transform it into a right-angled triangle pond and keep the trees in the same place?
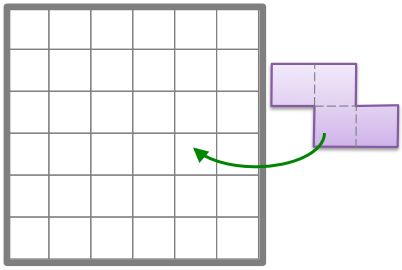How many colored four-unit shapes can be placed inside the 6x6 square without intersecting each other?
You may turn the shape.
Find the greatest number.
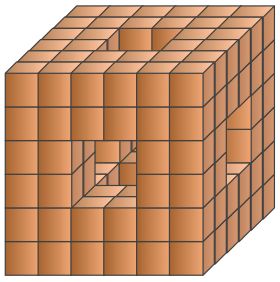A solid is a cube with three tunnels drilled through it, as you can see in the picture.
How many blocks are there in the solid?
Four matchsticks form a square.
How many non-overlapping squares can be formed using seven matchsticks?
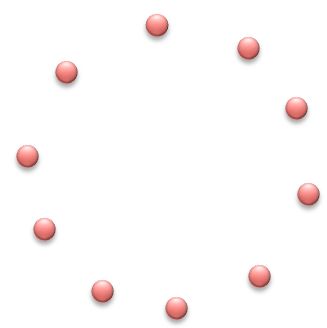Ten acrobats are evenly spaced at a circus circular arena.
Which acrobat is directly opposite the ninth performer?
It costs $24 to paint a cube.
Before painting, it was cut into eight cubes.
What is the cost to paint these small cubes?
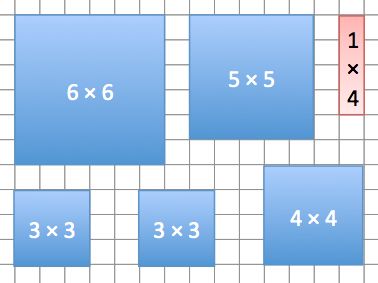Six shapes can be fitted together with no gaps and no overlaps to form a rectangle.
What is the smallest dimension of the rectangle?
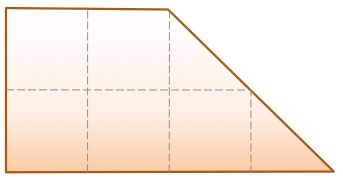I want to cut this shape into four pieces all of precisely the same size and shape.
Which is such a piece?
A rectangle floor 12 x 16 is covered by square tiles of sides 40 cm.
A chalk line is drawn from one corner to the diagonally opposite corner.
How many tiles have a chalk line segment on them?
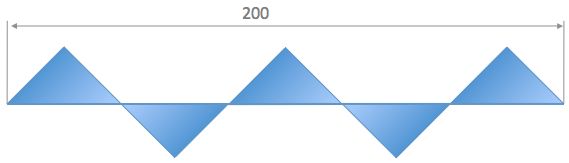The colored figure in the picture consists of identical isosceles right triangles.
What is the area of the blue shape?
A guard walks completely around the walls of a rectangular castle with a perimeter of 10 km.
From any point on his path, he can see exactly 1 km horizontally in all directions, except the wall.
What is the area of the region that contains all points that the guard can see during his walk?
In a triangle, the sum of two of the angles is equal to the third, and the lengths of the two longer sides are 17 and 15.
What is the length of the shortest side?
If the coordinates of one end point of a line segment are (1 , 2 , -3) and the coordinates of the midpoint are (-3 , 2, 1), what are the coordinates of the other endpoint?
What is the probability that a point chosen randomly from the interior of a rectangle is closer to the rectangle's center than it is to any of the rectangle's vertices?
Eight poles are evenly spaced on the circumference of a big circle.
What is the largest number of ropes that can be stretched between two poles so that no two ropes intersect at any point?
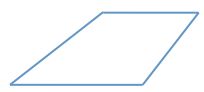A quadrilateral with one pair of parallel sides is referred to as a trapezoid.
A trapezoid has mutually perpendicular diagonals of lengths 4 and 6.
What is the area of the trapezoid?
An analog wristwatch says that the time is 14:20.
The minute hand moves 300 degrees.
How many degrees has the hour hand turned?
A curtain covers a window as shown on the right.
We approximate the area of the curtain by 2 triangles.
The window is 24 by 36 inches.
How much of the window area is covered by the curtain?
Which figure can be rotated 72° about its center and have its final orientation appear the same as the original orientation?
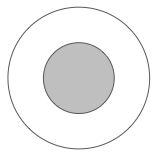In the diagram, the radii of the two concentric circles are 4.5 and 10, respectively.
What fraction of the bigger circle is shaded?
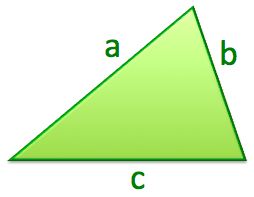If two sides of the triangle have lengths of 22 and 33, which of the following could be the perimeter of the triangle?
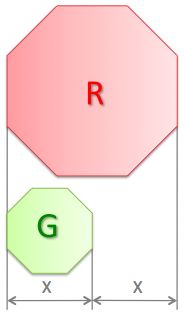If G is the total area of the green regular octagon and R is the total area of the red regular octagon, which is correct?
In a triangle, the sum of two of the angles is equal to the third.
The lengths of the sides are 12,13 and X.
Find X.
A telephone company places round cables in round ducts.
What position of the cables is the worst and demands using the round duct with the larger diameter?
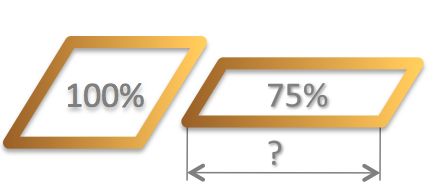Anna takes a rope that is 24 ft long and creates a square.
Bob takes the rope and creates a rectangle that has an area 75% of the square's area.
What is the length of the rectangle?
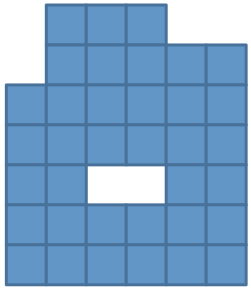Cut the shape into two pieces and create a square from them.
How many small squares are in the smaller of these two shapes?
What is the absolute difference between the largest and smallest possible areas of two rectangles that each has a perimeter of 100 units and integer side lengths?
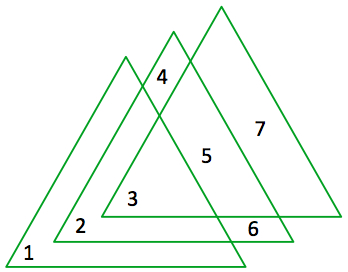Three equilateral triangles form seven unique regions.
What is the maximum number of regions that can be formed by three congruent, overlapping triangles?
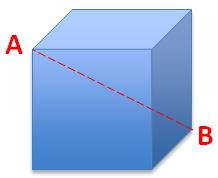I increase the cube so that the diagonal AB doubles its original size.
How many times does the volume increase?
I have a cube with a volume of 1000 cm3.
I make the length 20% longer, the width 10% shorter and the height 10% shorter.
What is the new volume?
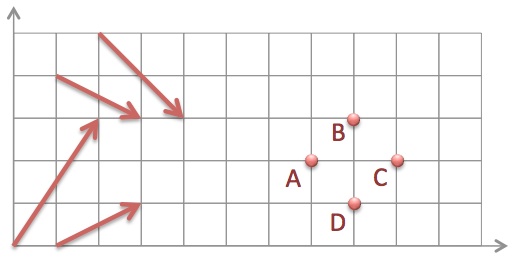If we add all these vectors and place the start of the resulting vector at the origin, where does the resulting vector end?
If I use 30 g of batter to make a crêpe of 30 cm in diameter, how much batter do I need for a 45-cm pancake of the same thickness?
"Archaeological evidence suggests that pancakes are probably the earliest and most widespread cereal food eaten in prehistoric societies." - Wikipedia
James the Mathematician just measured the angle of his piece of pizza, which is 39.6°.
What part of the pizza did James get?
A solar power station includes 17,000 mirrors, each 60m2.
What is the total area of the mirrors?
1 km = 1000m
The photograph courtesy of Roland Sauter
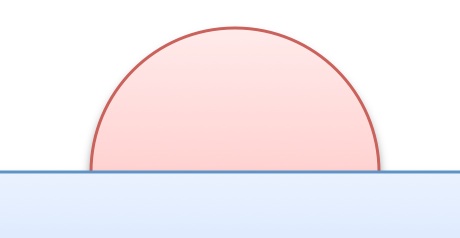Dr Heidi has been called in as an expert to solve a problem. There is a device which is spherical, air-tight when the two halves are glued together, and hollow; it is designed to be thrown into the sea and sit on the sea bed. When she asked them why they said it was hush-hush, top secret, need-to-know, ... and then they looked at her sternly. She hasn’t even seen it for herself. They said its diameter was &π (=3.1415926…) units, but they then said the units were Classified!
They said its weight is exactly 10kg. The sphere has plenty of air space inside.
What should she recommend to make the sphere sit on the sea bed?
Britain’s greatest inventor of mathematical puzzles Henry Ernest Dudeney asked you to place 12 mince pies in 6 lines with an equal number of pies in each line.
What is the largest possible number of pies in a line?
Marek, the pan-dimensional super being, has arbitrarily defined his current location as (0,0,0,0,0,0) in 6D hyperspace. He wishes to reach location (3, 0, 2, 0, 4, 3) by one of the many shortest paths available. Despite his immense power, he can only move one hyperstep at a time, each hyperstep consisting of a unit change in exactly one of the coordinate values. Any hyperstep is of equal ‘length’.
What is the smallest number of hypersteps required for him to reach his destination?
Author: Leslie Green
What is the minimum number of matches that must be moved in order to obtain exactly two equilateral triangles (with no left over pieces)?
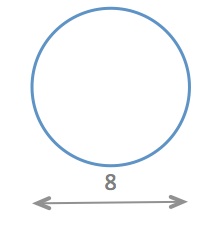What is the perimeter of a regular hexagon that perfectly fits into a circle with an 8-meter diameter?
I can draw 2 diagonals in a square.
How many diagonals can I draw in a hexagon?
There are 6 sides in a hexagon.
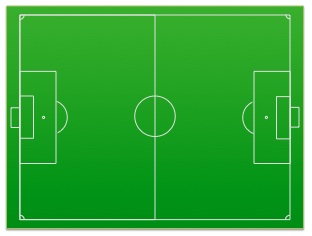The length of a soccer pitch is 110 meters and the width is 66 meters.
Before a match, ten ball boys are evenly spaced along 2 long sides of the pitch.
What is the maximum possible distance between the boys?
There are smaller squares inside the large rectangle.
If the green square has side length 1 and the red square has side length 3, what is the area of the large rectangle?
In how many ways can a square piece of paper be cut into two congruent shapes by a single straight line cut?
Pairs of identical rectangular strips, each measuring 5 by 1, are completely overlapped in a number of different ways to form different shapes.
What is the largest possible perimeter of the new shape?
A cellar floor is to be tiled in the way shown in the picture.
If the cellar measures 25 tiles x 27 tiles, how many green tiles will be needed?
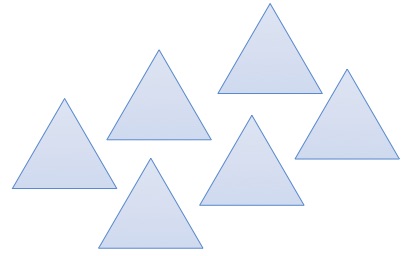A shape is made from 6 congruent equilateral triangles that share one, two, or three common sides.
What is the minimum possible number of sides the shape has?
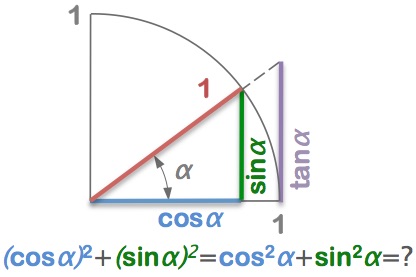There is a right angled triangle with a hypotenuse of unit length. Denote an angle (other than the right angle) as alpha.
Given that the side adjacent to the angle is of length cos(alpha) and the side opposite the angle is sin(alpha), evaluate the sum.
Author: Leslie Green
Gerry is running away from a horde of three wild animals. To escape, he always runs a dozen meters and then turns 90° to the left or to the right alternately.
Just before the seventh turn, what is his maximum displacement from the start?
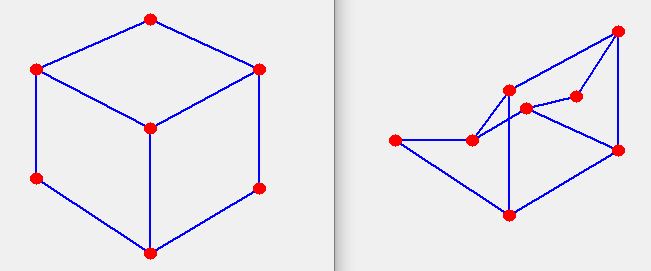Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Can you move the tennis balls from the pattern on the left to make the pattern on the right?
NOTE: the strings are special so that whatever you do they never get tangled up with each other.
Author: Leslie Green
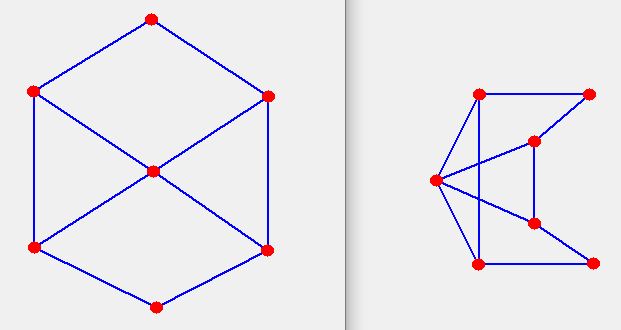Pretend the round red blobs are tennis balls. Pretend the blue lines are stretchy strings.
Can you move the tennis balls from the pattern on the left to make the pattern on the right?
NOTE: the strings are special so that whatever you do they never get tangled up with each other.
Author: Leslie Green
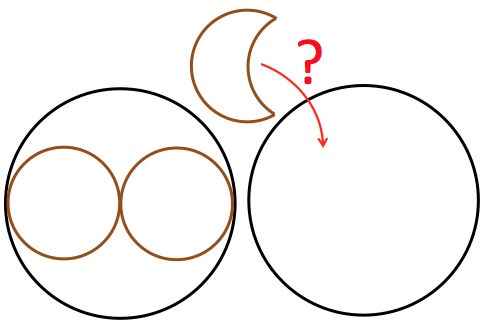A chocolatier can put only two circular chocolates (8-cm in diameter) in a circular black box which is 16.1cm in diameter.
How many moon-shaped chocolates fit in the box?
The moon-shaped chocolates have a diameter of 8cm and are formed by an arc of the same diameter that goes through the center (centre) of the circle.
Inspired by Alex van den Branhof, Jan Guichelaar, Arnout Jaspers Half a Century of Pythagoras Magazine. MAA 2011
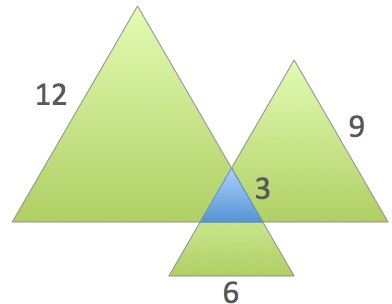The picture shows four equilateral triangles with sides of lengths
3, 6, 9 and 12.
How much greater is the green area compared to the blue area?
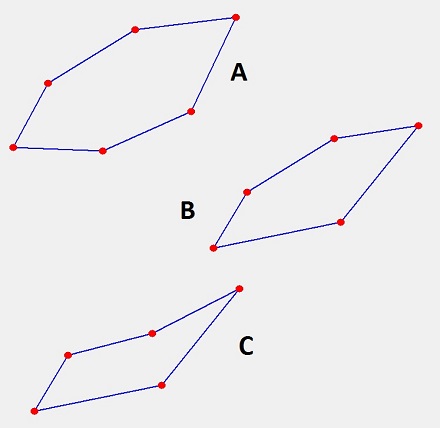Leslie Green asks:
A convex polygon is a simple polygon (not self-intersecting) in which no line segment between two points on the boundary ever goes outside the polygon.
Which of these shapes is not a convex polygon?
A piece of wire is to be cut into two parts in the ratio 7 : 8.
Each part is bent to form a square.
Estimate how much larger the area of the second square is compared to the first one.
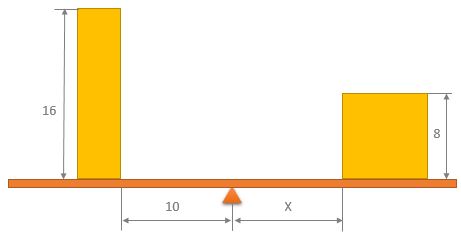The two blocks have identical weights, identical densities, and identical depths (into the page).
The second block is a cube.
What is the distance X to keep the system in equilibrium?
Pairs of identical rectangular strips are overlapped to form different shapes.
Which shape has the smallest area?
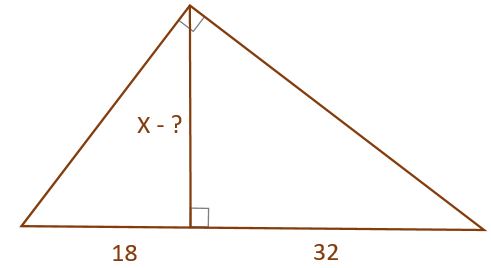The perpendicular X divides the hypotenuse of the right triangle into two segments of 18 and 32 feet respectively.
What is the length of the perpendicular?
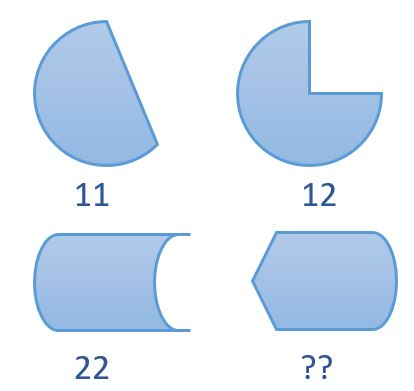MENSA question:
Using the first three shapes and values as a guide, find the value that corresponds to the last shape.
The measure of the two acute angles in a right triangle are in the ratio 2:7.
What is the measure of the smallest angle of the triangle?
Which shape could NOT be a cross section of a cone? 
What is the shortest path?
Which fraction of this triangle is shaded?
Three corners of a square are A(1,4), B(4,6), and C(6,3). 
How many red circles can be placed inside the blue circle without intersecting? 
Which side of this shape is 5 units long? 
The squares have side lengths of 2 and 4. 
How many planes of symmetry does an Egyptian pyramid have?
Find the line that splits the area of the ten squares into two equal parts. 
How many circles can be placed inside the square without intersecting each other?
The area of the smallest square is 124 square meters. 
For which capital letter of the English alphabet would you use the greatest amount of paint?
Every face of a cube has at least one white edge. 
A circle is inscribed in trapezoid. 
The circumference of each circle is 24 meters. 
What is the sum of the marked angles?
Four touching circles have the same radiuses. 
Which of the following could be the graph showing the area Y of a square with the side length X?
What is the greatest number of possible points of intersection of three circles?
The picture shows a regular pentagon and an equilateral triangle. 
How many inner right angles are possible in a hexagon? 
Find the sum of the five marked angles of a star that is inscribed into a circle. 
Find the angle between two diagonals drawn on two faces of the cube.
Which red piece can be put with the blue one to form a rectangle?
What is the area of the square? 
Identify two shapes with the same perimeter.
What is the perimeter of the triangle? 
If each edge length of this shape is tripled, what will happen to its volume? 
Which angle is largest?
Which shape is closer to the point (0,0) ?
How many right angles are possible in a polygon with six sides (hexagon)? 
Which triangle has angles that appear to measure 42°, 48° and 90°?
Calculate the area of the shape in small squares.
Estimate the size of the square if the circle diameter is 25 inches.
Which is the plan view of the 3-D shape?
Which two lines are perpendicular?
What is the volume of the figure, if X = 4? 
The blocks of ice are of the same height. 
Eugenia discovered round ink spots on her music paper. 
All three pathways consist of semi-circles. 
Find the maximum area of a rectangle that has a perimeter of 36 m.
What is the ratio of the reverse area of a dime to its circumference if its diameter is 18 mm?
Estimate the percentage of the circle area compared with the square area. 
What is the surface area of the cube if its side length is 3 cm?
Find X.
This rectangle has an area of 1 square meter. 
The shape is turned nine and half turns clockwise. 
Calculate the area of the shape in small squares.
Which two points have the largest distance between them?
Leslie Green asks: 
The right triangle is isosceles. 
What is the value of the marked angle in the regular star?
How much greater is the blue area compared to the yellow area?
Which integer is closest to 33&π?