Solve the simultaneous equations:
x – 4y = 0
x + y = 4
Find the sum of all the elements of this finite geometric sequence:
1, 2, 4, 8, 16, 32, 64, . . . , 1024.
Two candles are of the same height.
One burns in four hours, while the other burns in five hours.
When is one twice the height of the other?
In Morse code, each symbol is either a dot or a dash.
How many different sequences of 8 symbols are possible?
One apple and one banana together cost $3.
One apple and one carrot together cost $4.
One banana and one carrot together cost $5.
How much does an apple cost?
You have two buckets. The first bucket contains 5 liters of water and the second contains 5 liters of milk.
If you pour 1 liter of the water into the milk and then return 1 liter of the mixture to the water bucket, what are the proportions of milk to water in the first bucket?
I would like to write 1000 as n2 - m2, where n and m are positive integers.
Which number can be part of the solution for the problem?
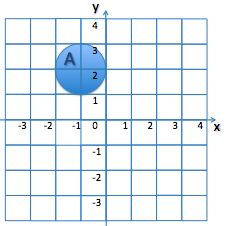A is the set of all points (x,y) in the shaded region.
Find the set B consisting of all points (2x, -y)?
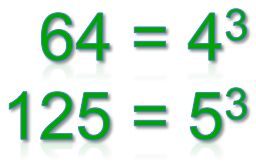A perfect cube is an integer whose cube root is an integer.
For example, 64 and 125 are perfect cubes.
A and B are perfect cubes.
Which of the following will NOT necessarily be a perfect cube?
100% of 90 girls and 90% of 100 boys have shown up in the concert hall on time.
10 teachers came even earlier.
What percentage of the people were late?
Divide 77 into three parts so that one is 150 percent of each of the other two.
What is the smallest number?
Engineers at a race company make three discoveries.
The first invention saves 50% of fuel, the second 30%, and the third 20%.
If the company uses all three innovations at once, how much fuel does a car consume compared with a normal car?
The average age of all teachers and students in a school is 15.
The average age of the teachers is 33.
The average age of the students is 12.
What is the ratio of teachers to students in the school?
One pipe can empty a pool 5 times faster than a second pipe.
When both pipes are opened, they empty the pool in five hours.
How long would it take to empty the pool if only the faster pipe is used?
The sum of the ages of four sisters is 30.
The sum of their ages four years ago was 15.
How old is the youngest sister?
A retailer offers a 25% discount off the normal price of a wooden puzzle.
She makes a profit of 25% over the cost of the puzzle.
What is her profit if the normal price of the puzzle is $20?
An outlet pipe can drain a full pool in 12 hours.
An inlet pipe can fill the empty pool in 8 hours.
The performance of the pipes does not depend on the water volume in the pool.
If both valves are opened, how long will it take to fill the pool?
A circle of radius 3 is drawn centered at the origin.
How many squares of side length 1 and integer coordinate vertices are inside the circle or intersect it?
Mrs. Smith puts $10,000 into a saving account that earns 2% interest compounded annually.
Which expression can be used to find the value of her money in the account at the end of the third year?
James has scored an average of 10 on his first 10 tests.
What score should he get in his eleventh test, so that his average moves up to 11?
Gerry earns 9% commission for each camera sold.
Today, he earned $44.1 commission.
What was his sales total for today?
In a shop, two liters of water costs $1, two liters of natural syrup cost $21, and two liters of the beverage that includes both costs $2.
The shop does not charge a premium for mixing the beverage.
What part of this beverage is the syrup?
If 15 students occupy 5/6 of the seats in the classroom, how many students would occupy 2/3 of the seats in the classroom?
Jane sets off from home to Boston at 50 miles per hour (mph).
Gerry sets off from home 30 minutes later.
What speed does Gerry choose in order to reach the same destination at the same time as Jane, given that he expects be there in 2 hours?
Find two positive integers that don't end in zero, and have a product of 1,000,000.
What is the smallest number?
Jane drinks only 2% fat milk. There are only 4% fat milk and 1% fat milk in a shop.
How many glasses of 1% fat milk does she mix with 1 glass of 4% fat milk to obtain her favorite composition?
390 people live on an island.
Eighty percent of men are married with women.
Each married couple has a child.
How many men live on the island if all women are married?
Jane earns two times as much per hour as Gerry.
Jane works 4 hours and Gerry works 6 hours.
They earn $210 in total.
How much do they earn per hour?
Please arrange 99 golden coins into 3 piles such that each pile has a different number of coins.
What will be the least number of coins in the largest pile?
The distance between Lausanne and Zurich is 200 km by rail.
Two trains, one from Lausanne to Zurich and another one from Zurich to Lausanne set off at the same time and travel at constant speeds.
If they meet 80 km from Lausanne, how much faster is the train from Zurich?
John's father is 4 times as old as John.
How many times older than John will the father be when John is twice as old as he is now?
Today is Anna's birthday. Her age today, in years, is equal to her age 11 years ago, in months.
What is her age today in years?
Four brothers share 2,400 coins left by their father.
How many coins will the eldest brother get if the second brother gets twice as many as the eldest brother, the third twice as many as the second brother, and the fourth brother twice as many as the third brother?
Sixty carpenters and forty plumbers work together.
The average daily rate of the workers is $240 while the average daily rate of a plumber is $300.
What is the average daily rate of a carpenter?
John weighs 112 pounds (lb) plus a half of Mary's weight.
Mary weighs 112 pounds plus a quarter of John's weight.
What is their combined weight?
Kids did push-ups every day for 7 days and the dog refused participating in the physical exercise.
Each day after the first day, Anna did one more push-ups than the day before. Bill always did twice as many as she did. In total they did 147 push-ups.
How many push-ups did Bill do on the last day?
A shopkeeper wants to create a cacao drink blend that has regular cacao powder mixed with premium cacao in a ratio of 5:4.
He already has a 90-kg mixture in which the ratio of regular to premium cacao is 4:5.
How many kilograms of regular cacao powder does he need to add to get his desired ratio?
One quarter of the competitors were faster than Jane and Mary, seven tenths of the competitors were slower than Jane and Mary.
How many girls were running?
Find the solution:
(x + 10) ( 4 - x) > 0
The notation
] A, B [
refers to the open-interval, A < value < B
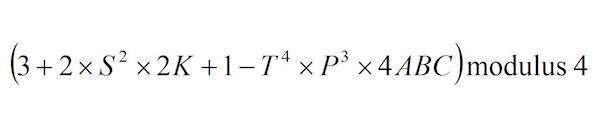Leslie Green asks:
Simplify the expression shown, if you dare!
All letters inside the bracket represent integer variables.
I weigh my three parrots in pairs because my balance only shows the correct weight if the mass is greater than 2 kg.
Buddy and Kiwi weigh 2.8 kg altogether.
Kiwi and Tiki weigh 2.4 kg altogether.
Tiki and Buddy weigh 3.2 kg altogether.
What is Kiwi's weight?
Herlewin the Lesser is trying to work out why his workers are costing him so much. He is paying 170 groats/hour for his workforce, consisting of one of each of a plasterer, an electrician, a carpenter, a builder, and an architect.
He knows that electricians earn twice as much as carpenters, that builders and plasterers earn the same, and that the carpenter and builder together earn as much as the architect. He also knows that the builder earns 30 groats/hour.
How much does the carpenter earn?
Author: Leslie Green
X x X = 2X
How many solutions does the algebraic equation have?
The symbol x is the multiplication sign (the times sign).
Eighty-five measures of corn must be divided among 4 peasants, such that the second peasant gets the same factor more than the first peasant, as the third gets more than the second, and as the fourth gets more than the third.
The puzzle is inspired by one of the most ancient math puzzles known on the Earth. About 1650 B. C., Egyptian scribe Ahmes, made a transcript of even more ancient mathematical scriptures dating to the reign of the Pharaoh Amenemhat III.
Image source of the Rhind Mathematical Papyrus : Wikipedia
The Big-Big gym has twenty-eight 2-kg and 5-kg disks for weight lifting.
The total weight of the 2-kg disks is the same as the total weight of the 5-kg disks.
What is the total weight of all the disks?
Jane visits her Grandma and then returns home by the same route. She walks 4km/h when going uphill, 12km/h when going downhill and 6km/h when on level ground.
If the one-way distance is 9km, then how much time does the trip take?
Four integer numbers
X, Y, Z, and Y / Z
are evenly divisible by 3.
Which of the numbers must be evenly divisible by 9?
Two ships are at a distance of 3 miles from each other. They each sail with a constant speed, while the first is twice fast as the second.
What are the shortest and the longest distances the first ship has to sail to intercept the second one?
The problem is derived from the Apollonius pursuit problem. The circle of Apollonius is any of several types of circles associated with Apollonius of Perga, a renowned Greek geometer.
You are required to follow my instructions very carefully:
After every mathematical operation you are to calculate the total.
Think of a number.
Add 3.
Multiply by 3.
Add 6.
Multiply by 2.
Subtract 30.
Divide by 6.
What is the result?
Author: Leslie Green
At one moment of a dance club performance 2/3 of the boys are dancing tango with 3/4 of the girls.
If there are 34 club members present, which represents a larger group at the performance?
The tango is danced in pairs, each consisting of one boy and one girl.
The great hero Bunny the Rabbit challenges a tortoise to a footrace. He agrees to give the tortoise a head start of exactly 1,199m. When the race begins, Bunny runs at a constant speed of 72 km per hour for exactly one minute and catches up the tortoise.
How far does the tortoise run?
One-fourth of the cars in a car park are 4x4.
Another car arrives and now one-third of the cars are 4x4.
How many 4x4 cars are now in the car park?
A gentleman who recently died left the sum of $380,000 to be divided among his widow, three daughters, and two sons.
The widow should receive three times as much as a son, and twice as much as a daughter.
What is her share?
Which statement is correct for 
Solve the equation: 
Which gives the largest answer if a = 11?
Solve 
Identify the location of point E under the transformation (x 2 + 3, y – 4).
Which equation represents line L?
Identify the point of intersection of the parallelogram's diagonals.
Find X
Find the expression that is INCORRECT.
Find X, if X > 0
How much does the maximum value of 
Find x.
The product of 4 consecutive integers is 840. 
Which point is closer to the origin (0,0)?
Which point does NOT belong to the line y = 3 + 0.25 x ?
How many numbers from 1 to 111 inclusive are equal to the cube of an integer?
What is the least positive integer n such that 
What number divided by 1001 is the same as that number minus 1001?
Find the last digits of the product. 
Which of the following green areas best represents the graph of the inequality 
The last digit of the number 444 is:
Anna used 189 digits to number the pages in her diary. 
What is x?
Find the value.
Which step is the flaw in the proof?
How many integer solutions does the expression have?
How many integer numbers are greater than 2016 x 2020 and smaller than 2018 x 2018?
The square root of half of a number is 5.