 John works 4-hour shifts at a call center.
John works 4-hour shifts at a call center.
He earns $4 per hour and $4 per call.
How many calls does he need to receive per shift to earn a total of exactly $400 in 4 shifts?
 John works 4-hour shifts at a call center.
John works 4-hour shifts at a call center.
He earns $4 per hour and $4 per call.
How many calls does he need to receive per shift to earn a total of exactly $400 in 4 shifts?
 Tom is choosing between two brands of AA batteries for his pocket flashlight. A package of two Brand A-Super batteries costs $4.99, and a package of two Brand B-Cool batteries costs $3.29. The runtime of the A-Super package is 2.5 hours. The runtime of the B-Cool package is 100 minutes.
Tom is choosing between two brands of AA batteries for his pocket flashlight. A package of two Brand A-Super batteries costs $4.99, and a package of two Brand B-Cool batteries costs $3.29. The runtime of the A-Super package is 2.5 hours. The runtime of the B-Cool package is 100 minutes.
Help him choose.
 A taxi company charges $1.75 for the first kilometer and 25 cents for each additional kilometer.
A taxi company charges $1.75 for the first kilometer and 25 cents for each additional kilometer.
What is the maximum distance someone could travel with seven dollars?
 If 9 workers can build 9 houses in 9 months,
If 9 workers can build 9 houses in 9 months,
then how many months would it take 11 workers to build 11 houses?
 Jim sells 80 percent of pineapples he had and throws away 10 percent of the remainder. On the next day, he sells two-thirds of the remainder and throws away the rest.
Jim sells 80 percent of pineapples he had and throws away 10 percent of the remainder. On the next day, he sells two-thirds of the remainder and throws away the rest.
What percent of his pineapples does Jim discard?
 If eight deciliters of Swiss apple juice, priced at $4.00 per liter, are combined with twelve deciliters of Italian apple juice, priced at $3.00 per liter, what is the price of the resulting mixture?
If eight deciliters of Swiss apple juice, priced at $4.00 per liter, are combined with twelve deciliters of Italian apple juice, priced at $3.00 per liter, what is the price of the resulting mixture?
 A space rocket has a critical fuel-control system protected by 4 fuel micro-controllers running together. If all 4 micro-controllers fail during the flight, the rocket will crash. The probability that any one micro-controller will fail is 1/5.
A space rocket has a critical fuel-control system protected by 4 fuel micro-controllers running together. If all 4 micro-controllers fail during the flight, the rocket will crash. The probability that any one micro-controller will fail is 1/5.
If the rocket has lifted off, what is the probability that it will not crash due to the fuel-control system?
 A carnival game offers you the opportunity to bet $1 on a number from 1 through 6 on a single roll of the two dice.
A carnival game offers you the opportunity to bet $1 on a number from 1 through 6 on a single roll of the two dice.
If your number comes up on one die, you win $2 and keep the $1 you bet.
If it appears on both dice, you win $5 and keep the $1 you bet.
Only if the number does not appear on either die do you lose your $1 bet.
Does this game favor you or the carnival?
Source: Mathematics Teacher, NCTM Journal
 Jane wants to buy a car.
Jane wants to buy a car.
The fuel efficiency is two times more important to her than the price of the car.
Help her to choose a car.
1 mpg (mile per gallon) = 0.425 kilometers per liter
The photograph courtesy of Roland Sauter
 9 farmers grow 9 apples trees in 9 years.
9 farmers grow 9 apples trees in 9 years.
How many years would it take for 999 farmers to grow 99 apple trees?
 A bicyclist pedals downhill at 20 km/h (kilometers per hour) and uphill at 10 km/h.
A bicyclist pedals downhill at 20 km/h (kilometers per hour) and uphill at 10 km/h.
It takes 4 hours to travel from a Swiss mountain village to another village.
The return trip takes 5 hours.
Find the distance between the two villages.
 You have eight dimes; seven are real and one is fake.
You have eight dimes; seven are real and one is fake.
All the real ones weigh the same, and the fake weighs less than the real ones.
How many times do you use a balance scale to find the fake dime?
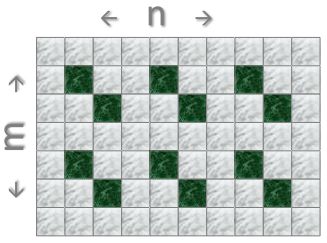 A city hall floor is to be tiled in the following pattern.
A city hall floor is to be tiled in the following pattern.
The hall measures 121 tiles x 61 tiles.
How many green tiles do we need?
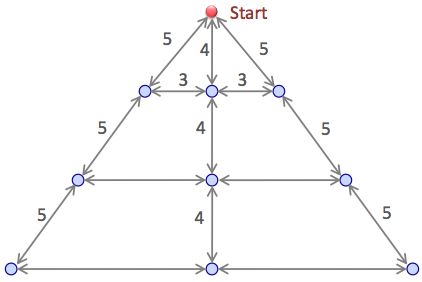 The traveling salesman problem: a salesman has to visit 9 towns and return home.
The traveling salesman problem: a salesman has to visit 9 towns and return home.
What is the shortest available route between the towns?
Any route chosen must lie on the paths shown. Paths with unmarked distances should be calculated from the geometry of map.
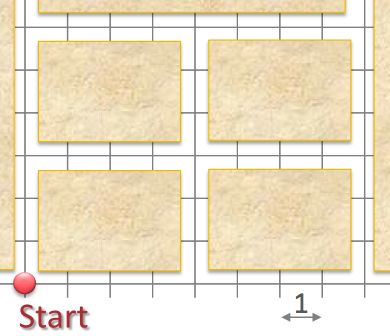 The Chinese postman problem: a postman wants to travel along each road in his quarter and come back to the Start.
The Chinese postman problem: a postman wants to travel along each road in his quarter and come back to the Start.
Find the minimal length of his route.
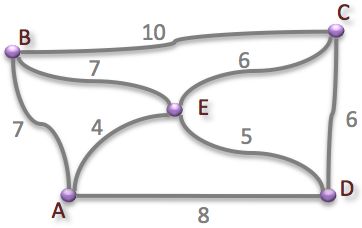 The diagram illustrates five villages, A, B, C, D, and E, with the distances between them in miles.
The diagram illustrates five villages, A, B, C, D, and E, with the distances between them in miles.
A postman must travel from A through each of the other villages exactly once and then back to A.
Identify the shortest possible route.
 The Legend of Carthage: Queen Dido and her followers arrived in North Africa.
The Legend of Carthage: Queen Dido and her followers arrived in North Africa.
The locals told them that they could have the coastal area that an ox hide would cover.
She cut the hide into a series of thin strips, joined them together, and formed a coastal shape.
The ox-hide enclosed area was known as Carthage.
If you had a 10 km long strip, which shape (rectangle, triangle, semi-circle, or semi-ellipse) would you choose to maximize the enclosed area?
 Anna can complete a project in 40 days.
Anna can complete a project in 40 days.
Bill can complete the project in 50 days.
Cindy can complete the project in 60 days.
Daniel can complete the project in 120 days.
Their daily wages are proportional to their performance.
Find 3 people who together complete the project in exactly 20 days.
 Choose the best advice for a strategic decision to the top management of a bank.
Choose the best advice for a strategic decision to the top management of a bank.
The profits stated are NET, in other words costs have already been deducted.
 You have 240 golden bricks identical in size and appearance but one is lighter than the others.
You have 240 golden bricks identical in size and appearance but one is lighter than the others.
How many times do you use a balance scale to find the odd brick?
 I am selling my car. People come to my garage one at a time and make bids to buy it. I make an immediate decision whether to accept or reject an offer after receiving it. I decide to reject the first N offers, mark the highest price P, and accept the first offer that is greater than P.
I am selling my car. People come to my garage one at a time and make bids to buy it. I make an immediate decision whether to accept or reject an offer after receiving it. I decide to reject the first N offers, mark the highest price P, and accept the first offer that is greater than P.
What value of N do you recommend to me if I expect that 270 people will make a bid?
If N is small, I can accept a small amount of money.
If N is large, I can reject the best offer.
 A goldfish needs 1000 cubic inches of water to live in.
A goldfish needs 1000 cubic inches of water to live in.
An aquarium is 20 inches in diameter.
How many goldfish can live in this aquarium?
 John's dad pays him $2 for each correct answer he gives in his math homework and fines him $8 for each incorrect answer.
John's dad pays him $2 for each correct answer he gives in his math homework and fines him $8 for each incorrect answer.
Today, John received nothing after doing 50 problems.
How many problems did John answer correctly?
 "Letter frequency. Accurate average letter frequencies can only be gleaned by analyzing a large amount of representative text." (source: Wikipedia)
"Letter frequency. Accurate average letter frequencies can only be gleaned by analyzing a large amount of representative text." (source: Wikipedia)
What is the most common letter in the English alphabet?
 I gave $120 to Brett, Cindy, and Daniel.
I gave $120 to Brett, Cindy, and Daniel.
Together Brett and Cindy received twice as much as Daniel.
Together Daniel and Cindy received three times as much as Brett.
Who received the most money?
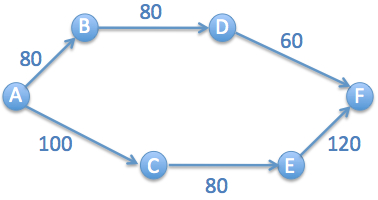 The diagram shows a road network.
The diagram shows a road network.
All cars drive in one direction from A to F.
The numbers represent the maximum flow rate in vehicles per hour.
Engineers want to construct a new road with a flow rate of 100 vehicles per hour. Drivers randomly choose the road at crossroads.
What new road decreases the capacity of the network (the number of vehicles at point F)?
 The Lucas problem.
The Lucas problem.
François Édouard Anatole Lucas (1842-1891) was a French mathematician.
Every day at noon, a ship leaves Le Havre for New York and another ship leaves New York for Le Havre. The trip lasts 7 days and 7 nights.
How many ships will a ship leaving Le Havre today meet at sea?
 A red-line subway train arrives at a station every 5 minutes and stays for 30 seconds.
A red-line subway train arrives at a station every 5 minutes and stays for 30 seconds.
A blue-line train arrives on the other side of the platform every 2.5 minutes and also stays for 30 seconds.
I randomly arrive at the station and always choose the train which arrives first, or any of the two if both trains are present.
What is the largest possible percentage of time that I take the red-line train?
 Four people arrive at a river at night. There is a narrow bridge, but it can only hold two people at a time. They have one torch and, because it is night, the torch has to be used when crossing the bridge.
Four people arrive at a river at night. There is a narrow bridge, but it can only hold two people at a time. They have one torch and, because it is night, the torch has to be used when crossing the bridge.
Person A can cross the bridge in one minute, B in two minutes, C in five minutes, and D in eight minutes.
What is the shortest time they all can get across the bridge?
Source : Wikipedia
 Every year, a man who had a million dollars at the beginning gives away half of his money to his son, and after that gives 20% of what he has left to charity.
Every year, a man who had a million dollars at the beginning gives away half of his money to his son, and after that gives 20% of what he has left to charity.
How much does he end up with at the end of the 5th year?
 The speed of a bus is 25 miles per hour (mph) including stops and 40 mph excluding the stops.
The speed of a bus is 25 miles per hour (mph) including stops and 40 mph excluding the stops.
For how much time does the bus stop in a 48-minute trip?
 Job interview logic puzzle in a bank.
Job interview logic puzzle in a bank.
Which of these pieces of information would be most useful for estimating the number of people who travel in a train with 20 passenger coaches?
 Wikipedia says that the equator is about 40,075 kilometers (24,901 miles) long; 78.7% is across water and 21.3% is over land.
Wikipedia says that the equator is about 40,075 kilometers (24,901 miles) long; 78.7% is across water and 21.3% is over land.
A yard was defined as the distance from finger tip to nose with the arms straight out to the sides.
Allowing 5 inches for a palm grip at each side we have 2(36-5) = 62 inches or 1.6m.
Estimate the number of people who holding hands in a human chain cover the length of the equator.
 In a game, Anna and Bill take 1, 2, or 3 coins on each turn.
In a game, Anna and Bill take 1, 2, or 3 coins on each turn.
The player to take the last coin from the pile wins.
If Anna goes first and there are 40 coins on the table, how many coins should she take to guarantee that she would win?
 John and Mary have square tiles with sizes 2 cm by 2 cm, 4 cm by 4 cm, 6 cm by 6 cm and so on.
John and Mary have square tiles with sizes 2 cm by 2 cm, 4 cm by 4 cm, 6 cm by 6 cm and so on.
Their kitchen is a rectangular room with a 224 cm by 288 cm surface.
What is the minimum number of tiles of the same size required to completely cover the surface without cutting the tiles?
 John and Mary have square tiles with sizes 5 cm by 5 cm, 10 cm by 10 cm, and 15 cm by 15 cm.
John and Mary have square tiles with sizes 5 cm by 5 cm, 10 cm by 10 cm, and 15 cm by 15 cm.
Their kitchen floor is a rectangle with a 230 cm by 440 cm surface.
What is the minimum number of tiles required to completely cover the floor surface without cutting the tiles?
 The size of a swimming pool is 25 x 12.5 meters.
The size of a swimming pool is 25 x 12.5 meters.
How many people must jump into the pool so that the water rises by 1 meter?
 If John walks up an escalator at a rate of one step per second, 12 steps take him to the top.
If John walks up an escalator at a rate of one step per second, 12 steps take him to the top.
If John goes up at two steps per second, he reaches the top in 20 steps.
How many steps are there on the escalator?
Inspired by A. Dunn, Mathematical Baffles, Dover Publications, 1980, p 17
 Two proofreading programs, A and B, discovered 30 and 40 errors, respectively.
Two proofreading programs, A and B, discovered 30 and 40 errors, respectively.
There are 10 errors in common.
Estimate the number of errors that are still undetected.
 Anna was planning to buy 10 souvenirs from the honesty shop.
Anna was planning to buy 10 souvenirs from the honesty shop.
She wanted some badges, which cost $5 each, and some Swiss chocolate bars, which cost $4 each.
After checking her wallet she decided to put 20% of the badges back.
How much money did she spend in the shop?
 Water is pumped into an empty swimming pool at a linearly increasing rate, which was zero at the beginning.
Water is pumped into an empty swimming pool at a linearly increasing rate, which was zero at the beginning.
If the pool is half full in 10 hours, how much extra time is needed to completely fill it?
 Twenty theater tickets for the first row were randomly distributed among 20 students.
Twenty theater tickets for the first row were randomly distributed among 20 students.
What is the probability that John gets a seat next to his true love Jenny?
 Two years ago, I bought a cottage for $800,000.
Two years ago, I bought a cottage for $800,000.
I was short of money and borrowed 12.5% of the money from a bank with 10% annual interest.
I sold it after two years and its value increased by 5% in that period.
What is my profit after I paid the bank back?
PS: I did not pay any tax for such a small transaction.
 Mrs. Brown bought 98 boxes of strawberries at $9 per box but 25 % of them were found to be rotten.
Mrs. Brown bought 98 boxes of strawberries at $9 per box but 25 % of them were found to be rotten.
She sells the non‐rotten strawberries.
What should the selling price per box be so that her profit is 50%?
 When I put 10 cubes of ice into my glass and they melt, the water doubles its volume and completely fills the 160 ml glass.
When I put 10 cubes of ice into my glass and they melt, the water doubles its volume and completely fills the 160 ml glass.
Estimate the size of a cube.
1 ml = 10mm x 10 mm x 10 mm
 A father has left 47 donkeys for you to distribute to his three sons;
A father has left 47 donkeys for you to distribute to his three sons;
1/2 (23.5) should go to his eldest son,
1/3 (15.667) to the middle one, and
1/8 (5.875) to the youngest.
You arrive with your own donkeys.
You can add or take some donkeys from the herd.
How do you divide them so that all sons are happy with your decision?
How many donkeys does the eldest son get?
Inspired by Malba Tahan “The man who counted.”
 Mary and John manage two different projects and they have a common budget.
Mary and John manage two different projects and they have a common budget.
Mary spent half of the budget, then John spent half of what was left, then Mary spent half of what was left and so on until the last cent.
What proportion of the budget did Mary spend?
 Management support accelerates the execution of a project by 10% during the first year of the project.
Management support accelerates the execution of a project by 10% during the first year of the project.
The same support delays the project execution by 10% during the second year.
Will the project execution take more or less time with management support?
 There are 190 people in a company including the project managers and CEO.
There are 190 people in a company including the project managers and CEO.
Project managers successively take out half of the total number of people to start a project until only the CEO is left.
How many project managers are there in the company?
 One by one, 40 cars enter a company parking lot with 40 assigned places.
One by one, 40 cars enter a company parking lot with 40 assigned places.
The first driver forgets his place number and takes a random place.
The remaining drivers take their assigned place, if available, or take a random place.
What’s the probability that the last driver ends up in his original assigned place?
Inspired by Peter Winkler's airplane problem.
 I see the reflection of the mountain peak 10 meters from me.
I see the reflection of the mountain peak 10 meters from me.
I know that the difference between the height of the lake and that of the peak is 1,800 meters.
How far from me is the mountain if I am 1.5 meters tall?
 An entrepreneur sells 1,250 tickets for a show, with 20% of them sold with 20% off.
An entrepreneur sells 1,250 tickets for a show, with 20% of them sold with 20% off.
How much does a normal ticket cost if the total income must be $120,000?
 A pirate boat is floating on a lake.
A pirate boat is floating on a lake.
The pirates throw a heavy chest with gold coins overboard.
What happens with the water in the lake with respect to the shore?
 A space rocket with 4 engines blew off one of them after one-month of flight.
A space rocket with 4 engines blew off one of them after one-month of flight.
It continued the flight at three-quarters of its former speed, which brought it to the destination two months late.
How long did the trip last?
 What is the minimum monthly salary you negotiate with your boss if you need
What is the minimum monthly salary you negotiate with your boss if you need
$1,800 per month to pay your house loan and its expenses,
$200 per week for yourself, and
$18,000 per year for leisure and saving?
PS: You pay 20% tax.
 What is the total surface area of 100 identical cubes which together have a volume of 51,200 cubic units?
What is the total surface area of 100 identical cubes which together have a volume of 51,200 cubic units?
This is a typical SAT question.
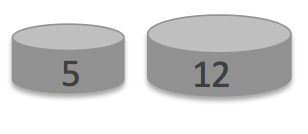 You have a large supply of 5kg and 12kg weights.
You have a large supply of 5kg and 12kg weights.
Six 5kg weights and one 12kg weight have an average weight of 6kg.
What is the minimum number of weights that have an average weight of 7kg?
 Gerry plans to swim a total of at least 1000 laps in January.
Gerry plans to swim a total of at least 1000 laps in January.
He swims every day except weekends (Saturday and Sunday).
He wants to increase the number of laps each day by one.
What is the least number of laps he must complete on the first weekday if January 1st is Monday?
 Texas experiences wide temperature fluctuations within a single day.
Texas experiences wide temperature fluctuations within a single day.
On January 1st, the temperature drops from 62° to 30° in Austin, and from 24° to 13° in New York.
What is the range within which the temperature difference between these two cities must be?
 James bought a new car for $30,000.
James bought a new car for $30,000.
Each year it depreciates (loses value) at a rate of 20%. The maintenance costs $3,000 the first year and it increases by 20% each year.
When does the maintenance cost exceed the value of the car?
 While eating out Gerry and Jim together tipped their server $7 in total.
While eating out Gerry and Jim together tipped their server $7 in total.
Gerry tipped 20% of his bill and Jim 15% of his bill.
Jim's bill was twice as much as Gerry's one.
They don't remember how much they paid.
Can you find the total including the tip?
 The water from an open swimming pool evaporates at a rate of 5 gallons per hour in the shade and 15 gallons per hour in the sun.
The water from an open swimming pool evaporates at a rate of 5 gallons per hour in the shade and 15 gallons per hour in the sun.
If the pool loses 8,400 gallons in June and there were no clouds, what is the average duration of night during that month?
 The limousine service makes 100 trips Center-Aeroport every day, each of which costs $50.
The limousine service makes 100 trips Center-Aeroport every day, each of which costs $50.
The company estimates that the number of trips decreases by 5 trips per day for each $5 increase in the fare and vice versa.
What fare is the most profitable for the company?
 I decided to use a password that includes 4 different numbers, with each number smaller than the previous one.
I decided to use a password that includes 4 different numbers, with each number smaller than the previous one.
How many options do I have?
 Gerry drives from his home to Jane's house at 50 mph.
Gerry drives from his home to Jane's house at 50 mph.
How fast must he make the return trip via the same route such that the average speed of the entire trip becomes 40 mph?
 Gerry gave half of his money to Jane.
Gerry gave half of his money to Jane.
Next day, she gave half of all her wealth to Gerry.
After the last exchange they each have exactly as much as they originally started with.
Who is richer?
 A district sends, on average, a total of 205 million gallons of water each month to its 20,000 residential customers.
A district sends, on average, a total of 205 million gallons of water each month to its 20,000 residential customers.
In the winter months, it sends an average of 100 million gallons per month.
Assuming the winter period lasts three months, what is the average number of gallons sent to each person in each nonwinter month?
 The manager of a company planned to distribute a $101 bonus to each employee from the company fund, but the fund contained $1 less than what was needed.
The manager of a company planned to distribute a $101 bonus to each employee from the company fund, but the fund contained $1 less than what was needed.
The manager gave each employee a $100 bonus and kept the remaining $199 in the company fund.
What was the amount of money in the company fund before any bonuses were paid?
 If you have a piece of paper that is 0.1mm = 0.01cm thick, how many times will you have to fold it in half in order for it to become as tall as me?
If you have a piece of paper that is 0.1mm = 0.01cm thick, how many times will you have to fold it in half in order for it to become as tall as me?
I am 163cm tall.
 There are 17 parallels and 12 meridians on a globe.
There are 17 parallels and 12 meridians on a globe.
Into how many areas is the surface of the globe divided?
 When Pinocchio lies, his nose gets twice as long.
When Pinocchio lies, his nose gets twice as long.
When he tells the truth, his nose gets 1 cm shorter.
His nose was 1 cm long in the morning, and it is 100 cm long in the evening.
What is the least possible number of times he opened his mouth today?
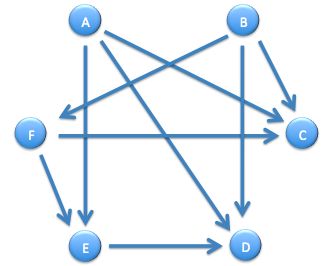 The diagram shows some of the results of a six-person contest. There are two matches left for everybody.
The diagram shows some of the results of a six-person contest. There are two matches left for everybody.
An arrow pointing from one player to another signifies that the first player defeated the second player in the match. For example, player A defeated player C in their match.
Which player has the strongest opponents left to play?
 A worker prepared a block for a pyramid in a day.
A worker prepared a block for a pyramid in a day.
If every day the number of workers doubled, how many days did they need to prepare 1000 blocks?
 A girl walked along a level road and up a hill from home and back.
A girl walked along a level road and up a hill from home and back.
Her pace on the level is 4 km an hour, uphill 3 km, and downhill 6 km.
How much time does it take if the total distance is 20 km?
Inspired by Lewis Carroll's Tangled Tale
 Eugenia wants to make a simple bridge for her dog. Currently he has to run through a tiny stream in the back garden and then walks mud into the house. Since Eugenia’s dad owns and runs a machine shop, she can easily get a single sheet of steel, aluminum or wood to bridge the stream.
Eugenia wants to make a simple bridge for her dog. Currently he has to run through a tiny stream in the back garden and then walks mud into the house. Since Eugenia’s dad owns and runs a machine shop, she can easily get a single sheet of steel, aluminum or wood to bridge the stream.
The length suits the size of the stream, the width suits the size of the dog, and the weight will be as much as she can carry.
The strength of a plain sheet is proportional to the relative strength of the material, its width and the cube of its thickness.
Which of the available materials makes the strongest bridge?
Suggested by Leslie Green
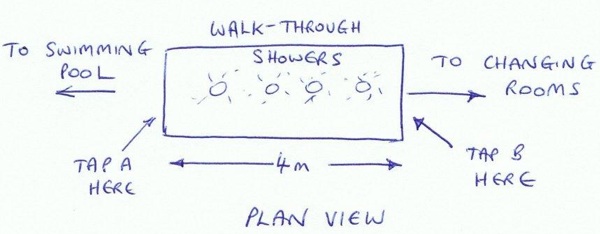 Now that I have made a vast fortune from my patented premium dog biscuits, I can afford to build the luxury mansion of my dreams.
Now that I have made a vast fortune from my patented premium dog biscuits, I can afford to build the luxury mansion of my dreams.
I thought my design requirement was very clear: The water for the walk-through shower can be turned ON and OFF from both ends of the room.
The plumber doesn't understand so I have drawn him a plan. I had a few attempts before I got it right!
Which is the correct drawing?
The problem was suggested by Leslie Green
 There are 10 coins and 5 of them are fake.
There are 10 coins and 5 of them are fake.
The real gold coins have the same weight, while all fake coins have different weights and each fake coin is lighter than a real one.
How many times do you use a balance to find all real coins?
Find the best strategy and the least possible number of weighings in the worst case.
 A train runs from Lausanne to Zurich at 100 km/hour without any stops and another one from Zurich to Lausanne at 80 km/hour.
A train runs from Lausanne to Zurich at 100 km/hour without any stops and another one from Zurich to Lausanne at 80 km/hour.
What is the distance between the trains 15 minutes after they meet each other.
 Shops have sales all the time to attract your business. Let the buyer beware! Not all sales are as good as others.
Shops have sales all the time to attract your business. Let the buyer beware! Not all sales are as good as others.
Given the same branded goods being sold, and the same quality of after-sales service, which shop offers the best value, given that two weeks ago all had the same price.
The problem was suggested by Leslie Green
 Leslie Green asks:
Leslie Green asks:
My neighbor John has invented a perpetual motion machine. It pumps water with no apparent power input and can even pump water up over a 2m fence.
How would you categorise this invention?
 Leslie Green asks
Leslie Green asks
"Suppose a particular nuclear waste material has a half-life of 100 years.
What could you do to reduce the radioactivity of the material itself to less than 7% of its current value?
(The half-life of a radioactive material is the time it takes, on average, for half of it to change into something else by spontaneous radioactive decay.)"
 Jane and Gerry compete in a best-of-five match.
Jane and Gerry compete in a best-of-five match.
If Gerry plays so that his girl-friend has a 75% chance of winning any particular game, what is the likelihood that she will win the match?
 There is a fault with the cruise control on Hank's car such that the speed continuously and linearly increases with time.
There is a fault with the cruise control on Hank's car such that the speed continuously and linearly increases with time.
When he starts off the speed is set to exactly 60 mph. He is driving on a long straight route with the radio on at full blast and he is not paying any attention to his speed. After 3 hours he notices that his speed has now reached 80 mph.
For how many miles did he drive above the state speed limit of 70 mph?
Author: Leslie Green
 Before his death, a rich man signed his will.
Before his death, a rich man signed his will.
"If my wife gives birth to a boy, she will get a third of $42,000,000 and my son will get two thirds of the money.
If my wife gives birth to a girl my wife will get two thirds of the money and my daughter will get one third."
After the rich man died, his beloved wife gave birth to twins: a boy and a girl.
What is the fair share of the money for the lady?
 Gerry promises to be at Jane's house at 19:00.
Gerry promises to be at Jane's house at 19:00.
If he bikes at 15mph, he arrives 1 hour earlier.
If Gerry bikes at 10mph, he is 1 hour late.
What is the speed to be exactly on time?
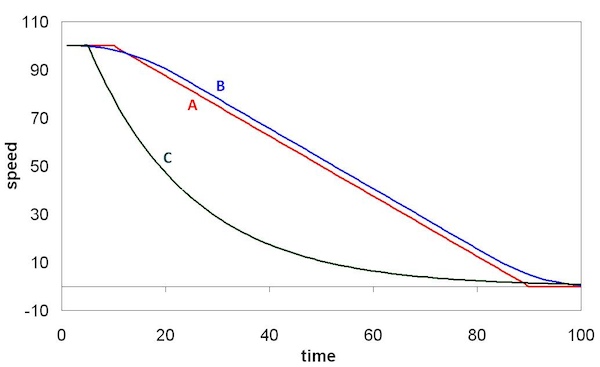 The train driver knows there is a Granny on board so he wants to give her a comfortable journey and to make sure she doesn’t spill her tea. When he is braking, which curve should he follow?
The train driver knows there is a Granny on board so he wants to give her a comfortable journey and to make sure she doesn’t spill her tea. When he is braking, which curve should he follow?
(HINT: remember Newton’s Second Law, often expressed as Force = Mass x Acceleration)
Author: Leslie Green
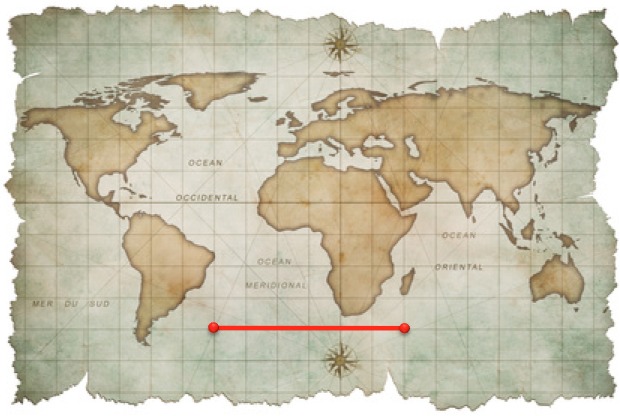 You may have heard the expression "The shortest distance between two points is a straight line."
You may have heard the expression "The shortest distance between two points is a straight line."
I have drawn a straight line on the map, directly along one of the grid lines of the map. Is this the shortest path for a ship to travel? (Neglecting winds, tides and so on.)
(NOTE: this is for a ship, not a submarine!)
Author: Leslie Green
 If $1,000 is invested in an account at 10% annual interest, how long will it take the account balance to grow to $1,600?
If $1,000 is invested in an account at 10% annual interest, how long will it take the account balance to grow to $1,600?
 Leslie Green asks:
Leslie Green asks:
Electrical energy can be measured in Joules, but for household use it is typically measured in kilowatt-hours (kWh). If a 100 Watt bulb is switched on for 8 hours every day for a year, roughly how much energy is consumed?
J = 1000 x kW x S
where J = Joules, kW = kilowatts, and S = seconds
 Leslie Green asks:
Leslie Green asks:
Suppose the light bulb in your fridge uses 1 Watt when on and you pay 10 cents = $0.1 per kWh.
Estimate the cost due to a faulty door switch, which keeps the light on over a 10 year period even with the fridge door closed.
(1 kWh is 1000 Watts for 1 hour)
 Leslie Green asks:
Leslie Green asks:
"A professional design standard requires that free standing equipment must not tip over if subjected to a force equivalent to one fifth of its weight applied at the worst possible point. The latest design has failed the test.
What can the design team do to fix the problem?"
 A taxi driver called John has 6-week annual holidays.
A taxi driver called John has 6-week annual holidays.
If the average fare is $17 and he usually manages to make 70 trips per week, what is his total income (before tax and expenses) for the whole year?
 A peasant bought a cow and a horse.
A peasant bought a cow and a horse.
Next day, he sold them for $1,800 each, making a loss of 20% on the cow and a profit of 20% on the horse. What did he make?
The photograph courtesy of Roland Sauter
 A 1-liter bottle contains a mixture that is 1/4 antifreeze, 3/4 water.
A 1-liter bottle contains a mixture that is 1/4 antifreeze, 3/4 water.
A 2-liter bottle contains a mixture that is 1/3 antifreeze, 2/3 water.
I pour the contents of the two bottles into my car's empty radiator.
What is the percentage of water in the radiator?
Note: Three liters of the liquid is not enough for a vehicle's radiator.
 Edgar chooses one of the double sheets of "The Daily Dog News".
Edgar chooses one of the double sheets of "The Daily Dog News".
The two internal page numbers of the sheet are 18 and 31.
How many pages are there in the newspaper?
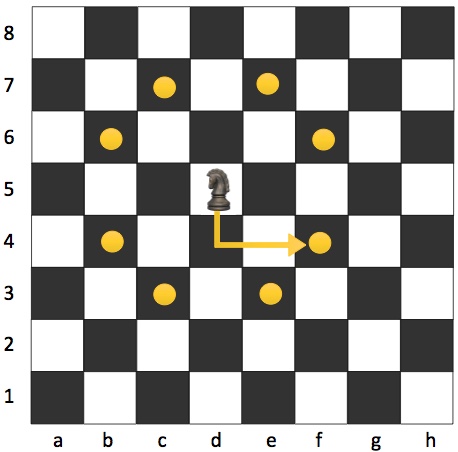 The knight jumps either 2 squares vertically and 1 horizontally, or 2 squares horizontally and 1 vertically, as shown in the picture.
The knight jumps either 2 squares vertically and 1 horizontally, or 2 squares horizontally and 1 vertically, as shown in the picture.
What is the minimum number of moves required for the knight to attack any square of the board from the current position?
 A cellar square floor is to be tiled in the way shown in the picture.
A cellar square floor is to be tiled in the way shown in the picture.
If the cellar size is extremely large, what is the percent of the green tiles?
 Jenny is a computer scientist and is shy about her age. On her birthday she encodes her age in binary in a row of 8 candles. Her boyfriend, who is sitting on the opposite side of the cake, is trying to work out her age from the pattern of lit candles.
Jenny is a computer scientist and is shy about her age. On her birthday she encodes her age in binary in a row of 8 candles. Her boyfriend, who is sitting on the opposite side of the cake, is trying to work out her age from the pattern of lit candles.
Knowing that her boyfriend is fluent in binary, Jenny encodes the pattern correctly, but does not reveal if a lit candle represents a “1” or a “0” for that bit position. She also does not reveal if she has written the binary number either left to right increasing (standard notation) or the other way around.
Given that Jenny is 27 years old, which age cannot reasonably be read by the boyfriend?
Author: Leslie Green
 If I start walking at my normal speed from home to my granny's house I will be 10 minutes late.
If I start walking at my normal speed from home to my granny's house I will be 10 minutes late.
If I run at twice my normal walking speed I will be 30 minutes too early.
After how much time do I need to switch from walking to running to arrive on time?
 Several students (N) randomly choose their places on a bench.
Several students (N) randomly choose their places on a bench.
What are the chances for Gerry to be sitting next to Jane?
 A dealer has 40 brand new cars to sell. He paid $40,000 per car. He hopes that half of the new cars will sell at the original price he sets, 40% of the remainder will sell later when their price is reduced by 10%, and the rest of the cars will sell in a clearance sale at only 80% of the original price. In order to make an expected profit, the total sales revenue must be $6,000 on average for each car.
A dealer has 40 brand new cars to sell. He paid $40,000 per car. He hopes that half of the new cars will sell at the original price he sets, 40% of the remainder will sell later when their price is reduced by 10%, and the rest of the cars will sell in a clearance sale at only 80% of the original price. In order to make an expected profit, the total sales revenue must be $6,000 on average for each car.
What original price should the dealer set?
 Eleven players are standing in a soccer pitch such that the distance between each pair is distinct. Each player has a ball, and when the trainer blows a whistle, each player kicks his ball to the nearest player.
Eleven players are standing in a soccer pitch such that the distance between each pair is distinct. Each player has a ball, and when the trainer blows a whistle, each player kicks his ball to the nearest player.
Which is not necessary true?
 The first four Volumes of an Encyclopedia are stacked vertically side by side on a shelf. The thickness of a Volume is 10cm, and the thickness of the two covers of each Volume is 1cm.
The first four Volumes of an Encyclopedia are stacked vertically side by side on a shelf. The thickness of a Volume is 10cm, and the thickness of the two covers of each Volume is 1cm.
What is the distance from the first page of Volume I to the final page of Volume IV?
 Sixty percent of people living on the left side of the Long Street vote for the Left Party and forty percent don’t vote.
Forty percent of people living on right side vote for the Right Party and sixty percent don’t vote. There are sixty percent more voters on the right side than on the left side.
Sixty percent of people living on the left side of the Long Street vote for the Left Party and forty percent don’t vote.
Forty percent of people living on right side vote for the Right Party and sixty percent don’t vote. There are sixty percent more voters on the right side than on the left side.
Who wins the election?
 Sixty percent of people living on the left side of the Long Street vote for the Left Party and forty percent don’t vote.
Forty percent of people living on right side vote for the Right Party and sixty percent don’t vote. There are sixty percent more voters on the right side than on the left side.
Sixty percent of people living on the left side of the Long Street vote for the Left Party and forty percent don’t vote.
Forty percent of people living on right side vote for the Right Party and sixty percent don’t vote. There are sixty percent more voters on the right side than on the left side.
If there are 780 voters on the Long Street, how many more people voted for the Right Party than for the Left Party?
 I take off from Brussels, Belgium and fly 777 miles due south. Then, I turn the plane and fly 777 miles due west. I turn again and fly 777 miles due north, and finally turn and fly 777 miles due east.
I take off from Brussels, Belgium and fly 777 miles due south. Then, I turn the plane and fly 777 miles due west. I turn again and fly 777 miles due north, and finally turn and fly 777 miles due east.
Which country do I land in?
 I insert 2 pins into a white paper covered board and connect them with a thread.
I insert 2 pins into a white paper covered board and connect them with a thread.
I take a pencil and draw a shape, always keeping the thread strained.
What is the shape?
 I have 100kg of potatoes, which are 99 percent water. I dry them until they are 98 percent water.
I have 100kg of potatoes, which are 99 percent water. I dry them until they are 98 percent water.
How much do they weigh now?
 Three identical airplanes (aeroplanes) set out on a vital mission. The lead plane is carrying a secret message which needs to be delivered by hand. Each plane has a full fuel tank and a 1200 mile range. The planes can transfer fuel in mid-air; this process loses no fuel and happens almost instantly.
Three identical airplanes (aeroplanes) set out on a vital mission. The lead plane is carrying a secret message which needs to be delivered by hand. Each plane has a full fuel tank and a 1200 mile range. The planes can transfer fuel in mid-air; this process loses no fuel and happens almost instantly.
How far can the lead plane get?
(Note that a plane with no fuel can still land safely.)
Author: Leslie Green
 Pop Quiz Paradox
Pop Quiz Paradox
A teacher announces to his class that there will be a quiz one day during the next week. The teacher gives the definition that they would not know when they came in to class that the quiz was going to be given that day.
The brightest student says that the quiz cannot be on Friday because they will know the day on Friday. With the same technique, she eliminates Thursday, then Wednesday, Tuesday and Monday.
"You cannot possibly give us a pop quiz next week," she says.
When does the teacher give the pop quiz?
I know the paradox from Charles Carter Wald. Probably, Martin Gardner described the quiz for the first time in The Colossal Book of Mathematics.
 This incident occurred in deep space. A space ship had been blasting its rockets at full power for several hours, such that the on-board accelerometers recorded an acceleration of 1g, the Earth normal gravitational acceleration of around 10m/s2. The Doppler Space Radar showed another space ship on a direct collision course so the Captain immediately cut off the engines. At this instant the other ship was 1000km away and a collision would happen in 1 hour if nothing was done.
This incident occurred in deep space. A space ship had been blasting its rockets at full power for several hours, such that the on-board accelerometers recorded an acceleration of 1g, the Earth normal gravitational acceleration of around 10m/s2. The Doppler Space Radar showed another space ship on a direct collision course so the Captain immediately cut off the engines. At this instant the other ship was 1000km away and a collision would happen in 1 hour if nothing was done.
What can you say with certainty about the speed of the other space ship?
Author: Leslie Green
 A 1 ton car is heading due North at 60 mph. A 2 ton truck is heading due East at 30mph. There is sheet ice all over the intersection and the truck cannot stop. The truck smashes into the side of the car and the pair forms one tangled mess of bent metal. (Fortunately the drivers were wearing seatbelts and the air bags did their job. Nobody was injured.)
A 1 ton car is heading due North at 60 mph. A 2 ton truck is heading due East at 30mph. There is sheet ice all over the intersection and the truck cannot stop. The truck smashes into the side of the car and the pair forms one tangled mess of bent metal. (Fortunately the drivers were wearing seatbelts and the air bags did their job. Nobody was injured.)
At what speed does the mangled mess initially travel?
(Hint: conserve momentum not energy).
Author: Leslie Green
 Three girls can complete writing four notebooks in five weeks.
Three girls can complete writing four notebooks in five weeks.
Four boys can complete writing five notebooks in six weeks.
How many notebooks can 10 boys and 11 girls complete in 12 weeks?
 In a company, the heights of all employees were measured. The average height of women was 168 cm, and the average height of men was 178 cm. Cindy was the tallest – her height was 180 cm. Zach was the shortest – his height was 152 cm.
In a company, the heights of all employees were measured. The average height of women was 168 cm, and the average height of men was 178 cm. Cindy was the tallest – her height was 180 cm. Zach was the shortest – his height was 152 cm.
A new employee came the next day. The average height of the women and the average height of the men did not change.
Among four conclusions below, only one can be drawn from this information with certainty. Which one?
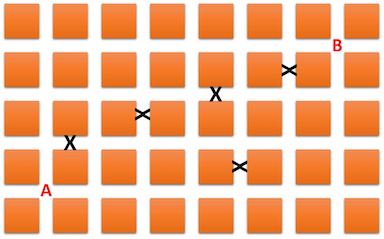 Gerry drives through the streets from crossroad A to crossroad B. Some of the streets are closed.
Gerry drives through the streets from crossroad A to crossroad B. Some of the streets are closed.
If he can only drive East or North, what is the number of different possible ways to get to crossroad B?
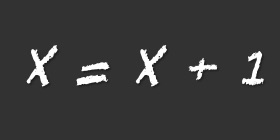 Leslie Green asks:
Leslie Green asks:
Jane sees the following text written on the blackboard in the classroom, evidently left over from a previous lesson.
X = X + 1
Which statement is true?
 Leslie Green asks:
Leslie Green asks:
In a singles tennis tournament of 64 players, the winner of each game goes forward to the next round. Two sisters are both excellent tennis players.
Given that each sister wins all their matches until they meet each other, what is the probability that they meet each other at the final?
 A secret service of a democratic country has 256 spies on payroll in a neighbor country. It is predicted that the network will increase the number of its spies by 25% each year.
A secret service of a democratic country has 256 spies on payroll in a neighbor country. It is predicted that the network will increase the number of its spies by 25% each year.
How many spies will the secret service have in four years?
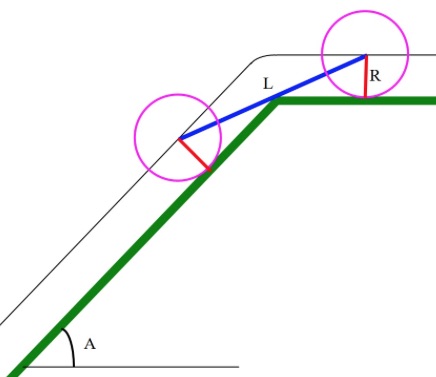 John got back to his car too late and now he is locked into an outdoor car park for the night. There is an escape path, but it involves driving down a fairly steep grassy slope. He has correctly drawn a diagram of the problem, but can’t quite finish it off. The axle of the wheels is roughly in line with the underside of the car. Hitting the underside of the car on the corner of the slope will mean a tow truck will be needed and there may be costly damage done as well.
John got back to his car too late and now he is locked into an outdoor car park for the night. There is an escape path, but it involves driving down a fairly steep grassy slope. He has correctly drawn a diagram of the problem, but can’t quite finish it off. The axle of the wheels is roughly in line with the underside of the car. Hitting the underside of the car on the corner of the slope will mean a tow truck will be needed and there may be costly damage done as well.
The faint line above the ground is the path that the car axle travels as it rolls along the ground. This is called the locus of the axle.
What is the correct equation for the limiting case where the car base just touches the corner?
Author: Leslie Green
 A motorboat is in the middle of a fast flowing river heading directly for some rocks that also happen to be in the middle of the river. Its engine failed 5 minutes ago so the boat is just being pulled along by the flow. Seeing the rocks in plenty of time the skipper pushes the rudder hard over to the left. The river channel is safe either side of the rocks.
A motorboat is in the middle of a fast flowing river heading directly for some rocks that also happen to be in the middle of the river. Its engine failed 5 minutes ago so the boat is just being pulled along by the flow. Seeing the rocks in plenty of time the skipper pushes the rudder hard over to the left. The river channel is safe either side of the rocks.
What happens next?
Author: Leslie Green
 It is a serious mistake to think that computers can solve any numerical problem almost instantaneously. Whilst addition and subtraction are very fast, multiplication can take twice as long as that, and division can take ten times as long as addition.
It is a serious mistake to think that computers can solve any numerical problem almost instantaneously. Whilst addition and subtraction are very fast, multiplication can take twice as long as that, and division can take ten times as long as addition.
In this example the values subscripted by N are to be calculated hundreds of thousands of times. The unsubscripted values are constants.
Rearrange the equation to minimise the computational time. We are after the form of the equation; the values of the constants vary as necessary to make the result correct.
Author: Leslie Green
 When representing negative whole numbers in binary for computers it is convenient to use the two’s complement form.
When representing negative whole numbers in binary for computers it is convenient to use the two’s complement form.
For example we could represent +3 as 0000 0011 in binary.
To get -3 in the two’s complement form we first invert the bits (change a ‘1’ to a ‘0’, and vice versa) and then we add 1.
Which is the correct two’s complement binary representation of -3?
Author: Leslie Green
 Kitty has one thousand beads, 777 of which glass and the rest are precious stones; 333 of them have a red tint.
Kitty has one thousand beads, 777 of which glass and the rest are precious stones; 333 of them have a red tint.
Estimate the probability that one randomly choosen bead will be a precious stone with a red tint.
 John, now aged 18, goes out to work for the first time. Since he is working, and an adult, he can eat whatever he wants. He likes sugary drinks, chocolate, and crisps. He also gets less exercise than he used to at school. As a result of this lifestyle, his food calorie intake averages out at 100 calories more than he needs every day. The human body typically stores excess calories as fat.
John, now aged 18, goes out to work for the first time. Since he is working, and an adult, he can eat whatever he wants. He likes sugary drinks, chocolate, and crisps. He also gets less exercise than he used to at school. As a result of this lifestyle, his food calorie intake averages out at 100 calories more than he needs every day. The human body typically stores excess calories as fat.
Given that a rough estimate of calories per pound of human body fat is 3500, estimate John’s weight increase by the time he is 28, all other factors being equal.
Author: Leslie Green
 For reasons best known to himself, John decides to get off the train before it comes to a complete stop. He jumps with both feet together in order to land well, although the height of the step is only a foot (30cm) off the ground. He makes sure to land facing in the direction of motion of the train. The train is moving at about 5 mph.
For reasons best known to himself, John decides to get off the train before it comes to a complete stop. He jumps with both feet together in order to land well, although the height of the step is only a foot (30cm) off the ground. He makes sure to land facing in the direction of motion of the train. The train is moving at about 5 mph.
What is the most likely outcome?
Author: Leslie Green
 There is a long distance hot-air balloon race. The winner will be the team that gets the furthest from the starting point. Each team consists of one or more team members. Each team member has a standardised weight by carrying ballast to make up to 150kg of load per person.
There is a long distance hot-air balloon race. The winner will be the team that gets the furthest from the starting point. Each team consists of one or more team members. Each team member has a standardised weight by carrying ballast to make up to 150kg of load per person.
Gas for the burner is provided with one standard bottle per person. The spherical hot air balloons use the same materials, but the balloons have a constant volume of hot air per person.
There are four teams: which one has the best chance, everything else being equal.
Author: Leslie Green
 You wish to establish how close to vertical a wall is. You have a spirit level and you can see that the bubble is not perfectly centred around its calibration marks when placed flat on the wall. Rotating the spirit level 180° about the vertical axis shows that the spirit level itself is essentially perfectly calibrated. In order to get the bubble centred you need to move the bottom of the spirit level about 1mm away from the wall. The spirit level is 30 cm long.
You wish to establish how close to vertical a wall is. You have a spirit level and you can see that the bubble is not perfectly centred around its calibration marks when placed flat on the wall. Rotating the spirit level 180° about the vertical axis shows that the spirit level itself is essentially perfectly calibrated. In order to get the bubble centred you need to move the bottom of the spirit level about 1mm away from the wall. The spirit level is 30 cm long.
What is the angular deviation of the wall from vertical?
Note: you do not have a calculator or trig tables to hand.
Author: Leslie Green
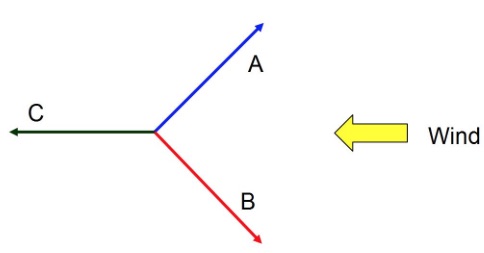 A modern sailing vessel, powered only by the wind, is at the center of the image (plan view).
A modern sailing vessel, powered only by the wind, is at the center of the image (plan view).
In which direction(s) can it travel?
Author: Leslie Green
 Much of the brilliance of aircraft design comes in optimising the ratio Lift/Drag for a range of flight speeds and conditions. In level flight the weight of the aircraft is equal to the Lift, but the retarding force, the Drag, is smaller by a factor of 10 or more. This means that the engine can produce 10x less thrust than would be needed to lift the aircraft straight up. Another key specification for a design is the Thrust/Weight ratio, a pretty self-evident measure.
Much of the brilliance of aircraft design comes in optimising the ratio Lift/Drag for a range of flight speeds and conditions. In level flight the weight of the aircraft is equal to the Lift, but the retarding force, the Drag, is smaller by a factor of 10 or more. This means that the engine can produce 10x less thrust than would be needed to lift the aircraft straight up. Another key specification for a design is the Thrust/Weight ratio, a pretty self-evident measure.
Analyse and digest this technical information before picking an answer.
Author: Leslie Green
 Peter has understood from his school work that an airplane's speed is relative to the wind, and not directly to the ground, so that if the wind is going in the same direction as the airplane, the airplane goes that much faster relative to the ground.
Peter has understood from his school work that an airplane's speed is relative to the wind, and not directly to the ground, so that if the wind is going in the same direction as the airplane, the airplane goes that much faster relative to the ground.
He therefore decides that it is a good idea to take off with the wind going in the same direction as his new model airplane is going to take off.
Comment on this plan.
Author: Leslie Green
 The heavy yellow weight is hung from the rigid red post. The blue plate is firmly attached to the ground with stakes (shown as thin vertical lines).
The heavy yellow weight is hung from the rigid red post. The blue plate is firmly attached to the ground with stakes (shown as thin vertical lines).
The joint at A is able to rotate freely.
What can you say with certainty about part B.
Author: Leslie Green
 Leslie Green asks:
Leslie Green asks:
Hopefully you realise that wood comes from trees. In fact the bulk of a tree is wood, along with a relatively small amount of leaves.
Where does all this wood come from?
(Pick the best answer, as some of the answers may be partially true.)
 The yellow point is the center of mass of the shaft.
The yellow point is the center of mass of the shaft.
If we cut it into two parts along the vertical line through the point, which part is heavier?
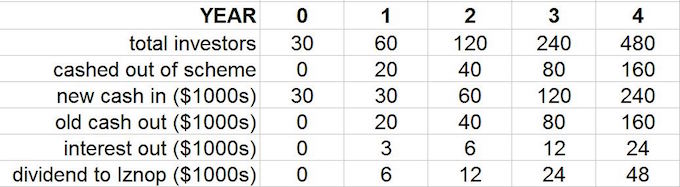 Carlo Iznop has an interesting business model for his investment firm. Each client deposits exactly $1000. He gives them 10% return on their investment after 1 year. This profit must be withdrawn. In the first year he had 30 clients. 2 out of 3 withdrew their money at the end of the year. At that time, word spread about this fantastic investment opportunity giving double the normal rate of return, so the total number of investors increased. Over the years his fame spread and the business boomed.
Carlo Iznop has an interesting business model for his investment firm. Each client deposits exactly $1000. He gives them 10% return on their investment after 1 year. This profit must be withdrawn. In the first year he had 30 clients. 2 out of 3 withdrew their money at the end of the year. At that time, word spread about this fantastic investment opportunity giving double the normal rate of return, so the total number of investors increased. Over the years his fame spread and the business boomed.
In the fourth year suspicions were raised about the consistently high profits and the police were called.
What is the most probable outcome?
Author: Leslie Green
 A thin-rimmed hollow sphere (a black ball) and a homogeneous solid sphere (a white ball) both have the same weight and the same diameter.
A thin-rimmed hollow sphere (a black ball) and a homogeneous solid sphere (a white ball) both have the same weight and the same diameter.
They are both dropped simultaneously from a height of 3 feet (around 90cm) onto a glass table below. Both balls have the same material and the same finish on their outer surfaces.
Which has the most kinetic energy at the moment of impact?
Author: Leslie Green
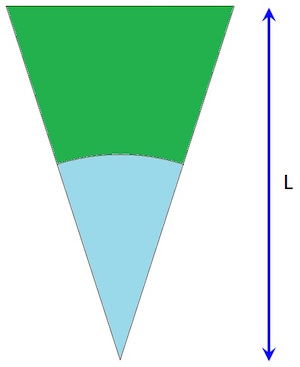 An eccentric retired professor of Mathematics has created a walled-off area in his garden in the shape of an isosceles triangle. He tethers a goat to the apex of the triangle with a rope of the correct length so that the goat can graze over exactly half of the garden.
An eccentric retired professor of Mathematics has created a walled-off area in his garden in the shape of an isosceles triangle. He tethers a goat to the apex of the triangle with a rope of the correct length so that the goat can graze over exactly half of the garden.
Neglecting practical considerations like the size of the goat compared to the garden, how long is the rope?
(This question comes in two variants: you can either approximate the answer or you can work out the complete answer - an only slightly more involved process.)
Author: Leslie Green
 A woman tries to hide her age from an inquisitive boy by telling him that her age is between 31 and 61 inclusive, but that the boy can only have 4 guesses at her age. The guess will be answered truthfully with higher, lower, or correct.
A woman tries to hide her age from an inquisitive boy by telling him that her age is between 31 and 61 inclusive, but that the boy can only have 4 guesses at her age. The guess will be answered truthfully with higher, lower, or correct.
In the worst (unlucky) case, but with intelligent guesses, how far from the correct age will the boy be?
Author: Leslie Green
 Four million people paid to watch the movie "Green Coat" in the first month the film was released on iTunes. Some paid $5 to rent the movie, and the rest paid $15 to buy it.
Four million people paid to watch the movie "Green Coat" in the first month the film was released on iTunes. Some paid $5 to rent the movie, and the rest paid $15 to buy it.
The total payments made were 30 million dollars.
The movie star Jake receives 20 cents from the rented film and 80 cents from the film that was bought.
What is Jake's revenue in the first month?
 Many houses in Switzerland use domestic air-sourced heat pumps for central heating.
Many houses in Switzerland use domestic air-sourced heat pumps for central heating.
A heat pump is a marvellous device. You can put 1kW (kilo-watt) of electrical power in and get 3kW of heat out. Engineers dislike calling this 300% efficient, so they use the term Coefficient of Performance (COP) instead. COP=3 means 3kW out for 1kW in.
Different manufacturers produce units with different performances, so under the same conditions one unit can have a COP of 3 and another can have a COP of 4.
Given the same conditions, how much more electricity will the COP=3 system require than the COP=4 system?
Author: Leslie Green
 Why would anyone design something as apparently stupid as a penny-farthing bicycle?
Why would anyone design something as apparently stupid as a penny-farthing bicycle?
And why would people buy it?
Author: Leslie Green
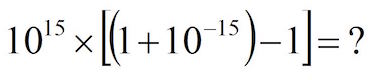 Leslie Green asks :
Leslie Green asks :
You try to work out the problem shown on the right by entering the values into a cheap hand-held calculator.
What answer do you get?
 Leslie Green asks :
Leslie Green asks :
Two ordinary cars with gasoline (petrol) engines are being compared. At their maximum power outputs, one produces twice the power as the other when measured at the road wheels.
What can you say with certainty?
 A girl takes 3 identical ropes, mixes the ends, and asks her boy-friend to tie three pairs of knots on the top.
A girl takes 3 identical ropes, mixes the ends, and asks her boy-friend to tie three pairs of knots on the top.
There is a superstitious tradition in their region that if the result is a ring with all three ropes, then their relationship will be long.
According to this tradition, what are chances of them getting a long relationship?
 You may have heard people use the expression "give it 110% effort" or similar.
You may have heard people use the expression "give it 110% effort" or similar.
What can you say about this?
Author: Leslie Green
 Jane has always been a bit of an oddball. Rather than buying stocks and selling them later, she likes to sell stocks she doesn't have, hoping to buy them back later.
Jane has always been a bit of an oddball. Rather than buying stocks and selling them later, she likes to sell stocks she doesn't have, hoping to buy them back later.
How does she make a profit?
Author: Leslie Green
 You have been offered a game of chance by an eccentric multi-billionaire.
You have been offered a game of chance by an eccentric multi-billionaire.
He will toss a coin repeatedly until it comes up heads. If heads appears on the first throw he will pay you $2. If it appears on the second throw, you receive $4; if on the third, you receive $8 and so on, doubling each time.
You know that this is the famous St. Petersburg paradox, with an expectation value of infinity, so his requirement for you to pay him $63 to play the game seems fair. And yet you hesitate …
What is the chance of you winning at this game?
Author: Leslie Green
 The blade of an engine is 1 meter long.
The blade of an engine is 1 meter long.
If it spins at a full rate of 2400 revolutions per minute (RPM), how many kilometers will the blade tip travel in one hour?
1 kilometer = 1000 meters
 Gerry has one hundred identical books. He puts some of them in a stack on the edge of a table.
Gerry has one hundred identical books. He puts some of them in a stack on the edge of a table.
What is the maximum horizontal distance that the edge of the top book can get from the edge of the table without falling over?
 As a green-minded driver, Gerry has a dilemma.
As a green-minded driver, Gerry has a dilemma.
He wants to buy a new eco model with emissions of 80 CO2 g/km instead of his current car that produces 120 g/km.
An article in the Telegraph says that production of a new car generates about 720kg for every £1,000 you spend on it.
The new car costs £20,000 and he usually drives 10,000 km every year.
How many years does he need to drive to make the purchase ecologically reasonable?
 Leslie Green asks:
Leslie Green asks:
In a popular type of train, a Diesel engine drives an electric generator, which in turns powers the electric motors that drive the wheels.
Given that every step in this chain loses power, why is such an apparently complicated system used?
Hint: If you drive or have been frequently driven in a 'stick-shift' (manual gearbox) car you will have a distinct advantage in answering this question.
 The safety label on this charger for power tool battery packs says 'Rest charger 15 minutes between charges'.
The safety label on this charger for power tool battery packs says 'Rest charger 15 minutes between charges'.
Why is there such a requirement?
Author : Leslie Green
 A horse trough has a rectangular cross-section and is continuously being filled from a tap. The trough has two similar holes in it: one at the bottom, and one half way up. The leak-rate from a hole is proportional to the square root of the water height.
A horse trough has a rectangular cross-section and is continuously being filled from a tap. The trough has two similar holes in it: one at the bottom, and one half way up. The leak-rate from a hole is proportional to the square root of the water height.
The tap is adjusted so that the water rises to one fifth the height of the trough as a steady-state condition.
The tap is now adjusted to double the flow rate. What is the new steady-state height of water in the trough?
Author: Leslie Green
 Joe, the ice-cream van man, has observed in his 20 years on the job, that almost all children like ice-cream.
In order to prove this he asks 999 of his child customers if they like ice-cream.
Joe, the ice-cream van man, has observed in his 20 years on the job, that almost all children like ice-cream.
In order to prove this he asks 999 of his child customers if they like ice-cream.
All but two say they like ice-cream.
What is the biggest problem with his assertion that around 99.9% of children like ice-cream?
Author: Leslie Green
 An elite special forces soldier weighing 100 kg (with full kit) is being winched up to a steadily hovering helicopter at a constant acceleration of 10 m/s2.
An elite special forces soldier weighing 100 kg (with full kit) is being winched up to a steadily hovering helicopter at a constant acceleration of 10 m/s2.
What is the steady-state load on the winch cable?
NOTE: take the gravitational constant as 10 N/kg or 10 m/s2
Author: Leslie Green
 A village lies in a mountain valley, with valley walls so high that the sun is blocked out for 6 months of the year. People can get very depressed when they live without sunshine for months on end.
A village lies in a mountain valley, with valley walls so high that the sun is blocked out for 6 months of the year. People can get very depressed when they live without sunshine for months on end.
At a council meeting it has been suggested that a mirror is installed on the valley wall to reflect sunlight onto the village below.
What would be the most useful response to the suggestion?
Author: Leslie Green
 Friday the 13th is considered an unlucky day in Western superstition.
Friday the 13th is considered an unlucky day in Western superstition.
What is the least number of Friday the 13ths that can occur in a calendar year?
 Leslie Green asks:
Leslie Green asks:
I have 8 books with weights of 1001g, 1003g, 1005g, 1007g, 1011g, 1013g, 1017g, and 1019g, where the weights are all accurate to better than ±0.1g.
I have a set of balance scales which will balance provided the imbalance is less than ±0.5g.
I weigh four books at a time, two on each side of the balance.
How many unique sets of 4 books will balance?
(Swapping books from the left pan to the right pan does not constitute another set.)
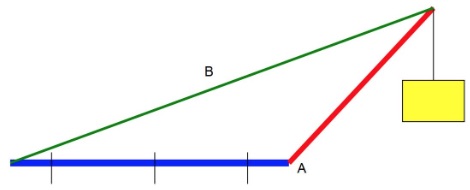
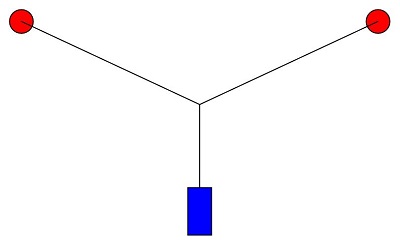 You have been told to suspend the blue object from one of the red mounting points. You have done some calculations and determined that one mounting point is only just inadequate to support that much load. The rope is easily strong enough, with plenty of margin, it is just the mounting point that is problematic.
You have been told to suspend the blue object from one of the red mounting points. You have done some calculations and determined that one mounting point is only just inadequate to support that much load. The rope is easily strong enough, with plenty of margin, it is just the mounting point that is problematic.
You boss really really wants the blue object suspended, NOW. He is a very important person and tells you to use two mounts as it will halve the load. The angle of the mounting ropes to the horizontal is 25°.
What is your response? (And remember, if anything goes wrong you were the engineer, and your boss is just a marketing expert.)
Just in case it is relevant: sin(25°) = 0.422; cos(25°)=0.906; tan(25°)=0.466
Author: Leslie Green
 Desmond the Dragon has been naughty. He has been burning cottages with his fiery breath and eating sheep between meals.
Desmond the Dragon has been naughty. He has been burning cottages with his fiery breath and eating sheep between meals.
The villagers have decided this must stop, so they have tied him up with a tungsten cable which can hold twice Desmond's weight.
Is this an adequate precaution?
Author: Leslie Green
 Lenny throws a baseball to Kenny who is 20m away. The ball arrives in 500ms (0.5s).
Lenny throws a baseball to Kenny who is 20m away. The ball arrives in 500ms (0.5s).
Neglecting wind resistance and taking g = 10m/s2, how fast is the ball thrown, given that it is thrown from and received at the same height?
Although you may use different symbols, these formulae may provide some reminders:
s =ut + (1/2)at2 ; v2 - u2 = 2as ; v = u + at
Author: Leslie Green
 Leslie Green tells a story and asks:
Leslie Green tells a story and asks:
The year is 2045. Most new cars now have electric drive trains. One particular new innovation is the DriverTron with its Insanity Mode. In this mode the car automatically applies a constant maximum power to the wheels at all speeds until it reaches 100mph or until the brakes are applied. Needless to say this mode has been banned in all jurisdictions apart from two States in the USA!
If we neglect wind resistance and bearing loss, what equation represents the velocity v of the car in Insanity Mode at speeds less than 100mph?
t is the time from starting at zero speed, and k is a constant.
 Rechargeable battery technology is familiar to most people with phones and other portable devices. But larger batteries to power cars and homes are less well understood.
Rechargeable battery technology is familiar to most people with phones and other portable devices. But larger batteries to power cars and homes are less well understood.
A rechargeable battery can be modelled as an ideal rechargeable battery in series with a parasitic resistance. This resistance dissipates power dependent on the square of the charging current. Now given that electric cars typically have a range of only 200 miles, it is quite tiresome to stop every 150 miles and recharge it for 300 minutes (5 hours). It would be much nicer to charge it in 30 minutes, or even 3 minutes, to make it more like a gasoline (petrol) powered car. But is there a downside to this?
We are going to assume for simplicity that a rechargeable battery is charged by a certain number of ampere-hours. If you double the current (measured in amperes) you halve the charging time.
Consider what happens to the energy loss in the parasitic resistance in the battery if instead of charging in 300 minutes you use a hyper-charger and do it in 3 minutes (for the same battery type).
Author: Leslie Green
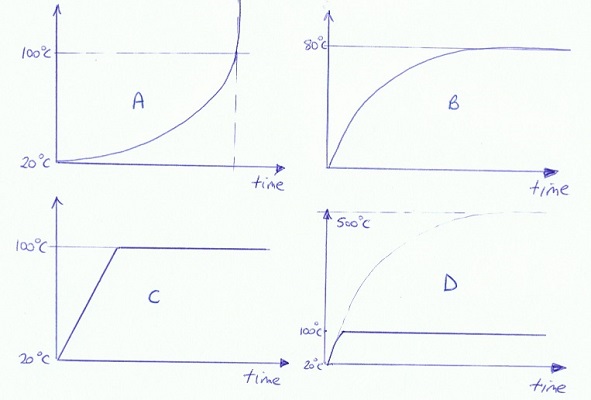 A Physics teacher is on a camping trip with his young nephew. Seizing the opportunity to impart some Physics to this youth, the teacher sketches out a graph of how well-stirred water in an open pan might respond to being placed in the middle of a well-established large fire, built using locally sourced wood.
A Physics teacher is on a camping trip with his young nephew. Seizing the opportunity to impart some Physics to this youth, the teacher sketches out a graph of how well-stirred water in an open pan might respond to being placed in the middle of a well-established large fire, built using locally sourced wood.
Which graph did he draw?
(Note: you must be able to justify your answer to get full credit on this question.)
Author: Leslie Green
 Suppose you were travelling directly from the Earth to the Moon. You can imagine that as you got further from the Earth, the pull of Earth's gravity would be reducing, whilst the pull from the Moon's gravity would be increasing. At some point these two forces would be equal and opposite.
Suppose you were travelling directly from the Earth to the Moon. You can imagine that as you got further from the Earth, the pull of Earth's gravity would be reducing, whilst the pull from the Moon's gravity would be increasing. At some point these two forces would be equal and opposite.
At what fraction of the distance from the Earth to the Moon would this equilibrium point be?
For the purpose of this question, assume that only the Earth and the Moon exist, and that they are stationary. Take the mass of the Moon to be 1/100th the mass of the Earth.
And we will remind you that the gravitational force on a small object is proportional to the mass of the astronomical body, and inversely proportional to the square of the distance to that body.
Author: Leslie Green
 Whilst the Earth gets all of its heat from the Sun, roughly how much of the Sun's heat does the Earth get?
Whilst the Earth gets all of its heat from the Sun, roughly how much of the Sun's heat does the Earth get?
Don't over-complicate the question. Just think about how much of the Sun's radiated power is intercepted by the Earth.
Sun's diameter = 1.4 million km
Earth's diameter = 13,000 km
Distance to the Sun = 150 million km
Author: Leslie Green
 A spaceship is going to fly from the Earth to Mars. The project has been sabotaged by politicians so that the flight starts when the planets are in the worst possible orientation for the flight.
A spaceship is going to fly from the Earth to Mars. The project has been sabotaged by politicians so that the flight starts when the planets are in the worst possible orientation for the flight.
What is the distance the spaceship has to travel?
Assume circular orbits with a common center (centre) about the Sun. Assume both orbits are in the same plane. Don't worry about matching orbital velocities.
Radius of the orbit of Mars = 230 million km.
Radius of the orbit of Earth = 150 million km.
Author: Leslie Green
 Americans currently average 6.8 hours of sleep at night, down more than an hour from 1942.
Americans currently average 6.8 hours of sleep at night, down more than an hour from 1942.
On average, Americans spend just 90 minutes eating during the day.
American adults are watching television five hours per day on average.
The average man employed full-time works 8.4 hours per work day.
Bob, a typical American, shaves himself and spends the necessary time in the bathroom, amounting to 18 minutes per day. He goes to work and back in 1 hour.
How much time does he have left for his family, leisure, Internet, and helping his beloved wife Mary on a day when he works?
 How should you split a 125-dollar check (bill) without tax in a restaurant among 5 friends?
How should you split a 125-dollar check (bill) without tax in a restaurant among 5 friends?
Remember to add 8% tax, to tip 15% after the tax and round to dollars.
 Aplusclick website had about 120,000 visits per month in 2017. At such websites, the visitors click on ads in 30 cases out of 1000 exposed pages on average.
Aplusclick website had about 120,000 visits per month in 2017. At such websites, the visitors click on ads in 30 cases out of 1000 exposed pages on average.
A dominant Internet search leader pays as little as $0.10 per click.
Aplusclick team thinks that any ads disturb visitors. The team excludes advertising on the website.
What was the annual revenue the team missed in 2017 by excluding the ads?
 You wish to pour juice into a glass from a container with a rectangular cross-section (as shown).
You wish to pour juice into a glass from a container with a rectangular cross-section (as shown).
We can define the orientation of the container by saying that one of the 4 marked edges is uppermost.
Which edge should be uppermost to give the best control when pouring from a fairly full container?
Author: Leslie Green
 Every day over a period of 10 days ten boys each sent a love letter to their unique and special girlfriends.
Every day over a period of 10 days ten boys each sent a love letter to their unique and special girlfriends.
John always writes to Rosy, Pete always writes to Jade, Steve always writes to Celeste, and so on.
The postman put the letters into ten different boxes without looking at the name of the recipient.
What is the expected number of letters that reached the correct recipient?
 Leslie Green asks:
Leslie Green asks:
The image shows a wooden door with a brush-type draft excluder ready to be cut to fit on the bottom of the door. The door hinge is on the left in this picture.
The instructions that come with the part just say to cut it to size, but where should we cut it?
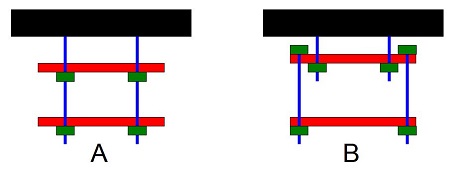 Drawing A shows a massive black beam easily supporting the load of two heavy red beams by means of the blue tension rods and the green nuts. The blue rods are very strong, while the nuts are the weakest elements of the design. It is not your design, but you have been given computer simulations of this design and it all looks fine, ... in theory.
Drawing A shows a massive black beam easily supporting the load of two heavy red beams by means of the blue tension rods and the green nuts. The blue rods are very strong, while the nuts are the weakest elements of the design. It is not your design, but you have been given computer simulations of this design and it all looks fine, ... in theory.
The contractor hired to build the design hates it. The green nuts have to be spun all the way up the blue threaded tie rods, which is very time consuming and therefore expensive. Also both red bars have to be assembled at the same time and that is difficult. The contractor has come up with design B which uses shorter tie rods of the same design but uses the same nuts. They have calculations to show that the upper red beams will not be damaged by offsetting the lower tie bars slightly.
Will you approve the change?
Author: Leslie Green
 You spin a wheel and it randomly lands on a money sector or END. If you land on a money sector you get the money and spin the wheel again. You keep receiving money until you land on END.
You spin a wheel and it randomly lands on a money sector or END. If you land on a money sector you get the money and spin the wheel again. You keep receiving money until you land on END.
How much do you expect to win on average?
 In a Math country, a young man dates a girl until they decide to marry or to split.
In a Math country, a young man dates a girl until they decide to marry or to split.
If they split, he dates another girl.
The girl does the same.
There is 50% chance that the man is ready to marry. The same probability applies to the girl.
Estimate the number of girls a young man dates before he marries one.
By the way, the expected number is the same as the expected number of boys a young girl meets before her marriage.
 A rich father has 71 camels. He promises at least 1/2 of the camels to the oldest son, at least 1/3 to the middle son, and at least 1/9 to the youngest son.
A rich father has 71 camels. He promises at least 1/2 of the camels to the oldest son, at least 1/3 to the middle son, and at least 1/9 to the youngest son.
He wants to give several camels to his daughter.
What is the maximum number of camels he can give to his daughter and still keep his promises?
 Leslie Green asks:
Leslie Green asks:
This is a UK mains socket, nominally rated at 230 V AC, 13 A (3 kW)
When is it most likely to catch fire?
 Leslie Green asks:
Leslie Green asks:
Desmond von Dummkopf is showing off to his (so-called) friends again. He is going to ride his unicycle over the strong concrete structure shown.
(5 m/s is roughly 11 mph.)
Does he have any chance of making the jump?
(We only consider the jump, not the ability to hold the unicycle upright during and after the landing --- if he should succeed in getting to the other side.)
g = 10m/s2
 Leslie Green asks:
Leslie Green asks:
The sketch to the right suggests the outline of a wire-frame bird-cage. The wire is thin, with large gaps, so the bird can easily see in all directions. The cage is supported by a single cord (red). The size of the bird is very small compared to the size of the cage.
As an experiment we hang the red cord from an electronic force sensor to measure the weight of the bird plus the cage.
What happens to the measured weight when the bird flies around?
 In one of the many different types of domestic heating systems, hot water is pumped around the house and heats rooms via "radiators".
The fact that the dominant heat transfer mechanism is actually convection, rather than radiation, is easily demonstrated by putting your hand just above the radiator and just below. It is of course much hotter above the radiator, showing that convection is dominant.
In one of the many different types of domestic heating systems, hot water is pumped around the house and heats rooms via "radiators".
The fact that the dominant heat transfer mechanism is actually convection, rather than radiation, is easily demonstrated by putting your hand just above the radiator and just below. It is of course much hotter above the radiator, showing that convection is dominant.
Why is it necessary (and recommended) to turn up the water temperature in the boiler and radiators during the cold winter months?
Pick the most accurate answer.
 It is easy to show that making beams long in the direction of the load makes them disproportionally stiffer.
It is easy to show that making beams long in the direction of the load makes them disproportionally stiffer.
We have a simple wooden rod with a square cross-section. Let's suppose it has a 2cm x 2 cm cross-section and is 1m long for the sake of clarity. One piece of this wood is not stiff enough for our purposes, so, knowing the stiffness equation, we stack three pieces up vertically. The three rods together now have a cross-section of 2cm x 6cm with the rods stacked upwards (the direction of the load), not sideways.
How much stiffer is this new assembly compared to the original rod?
The problem was suggested by Leslie Green.
WARNING: Do not try bending any beams like this without using eye protection. Certain rulers are known to shatter and eject bits of plastic into nearby eyes.
 PCR (Polymerase Chain Reaction) is a technique used to make copies of a particular section of DNA. It is therefore also referred to as DNA amplification.
PCR (Polymerase Chain Reaction) is a technique used to make copies of a particular section of DNA. It is therefore also referred to as DNA amplification.
A PCR machine heats the sample (along with various other ingredients) up to 96°C to split the DNA strands, cools it to around 60°C to allow binding to the separated DNA strands, then heats it up to 72°C to complete the copying process. Because DNA is a double helix, and each side is copied, each PCR cycle roughly doubles the amount of the DNA section present.
If we start with one DNA chain, how much would we expect after 30 PCR cycles?
by Leslie Green
 John lives in a fairly well-insulated fairly old brick-built house in a central European location. In the winter the weather gets quite cold at night compared to the day.
John lives in a fairly well-insulated fairly old brick-built house in a central European location. In the winter the weather gets quite cold at night compared to the day.
Peter lives in a much newer brick-built house in the same village as John. The locations of the two houses in terms of local climate and wind are similar.
John turns off the heating between the hours of midnight and 6am to save money on his heating bill. Peter claims that John is wasting money on his heating bill because John has to keep heating up the walls every day, rather than leaving them at a more even temperature. Peter has evidence that his scheme of leaving the heating on all night is better since his heating bill is 10% lower that John's; their houses are similar sizes, and kept at the same sort of temperature.
Which scheme saves the most on energy costs?
by Leslie Green
 There is a new and dangerous strain of bacteria in town. You have a total of 10 anti-biotics and supplements available, but you have been told that they are all individually ineffective. You hope that some combination of them may be effective, and you also hope that when testing, the relative amounts of each constituent is not critical.
There is a new and dangerous strain of bacteria in town. You have a total of 10 anti-biotics and supplements available, but you have been told that they are all individually ineffective. You hope that some combination of them may be effective, and you also hope that when testing, the relative amounts of each constituent is not critical.
Fortunately you have a fully automated sample handling facility at your disposal, so you can make as many tests as you want, and the computerized system can tell if the result is a success without your intervention. It is the nature of such tests that the sample needs to be incubated for 24 hours to see if it has been successful.
How long will it take to fully test your idea?
by Leslie Green
 Americium-241 is a radioactive isotope with a half-life of 432.2 years. It is widely used in domestic smoke alarms in the form of Americium-241 dioxide.
Americium-241 is a radioactive isotope with a half-life of 432.2 years. It is widely used in domestic smoke alarms in the form of Americium-241 dioxide.
Estimate how much of the Americium has decayed at the end of the typical 10 year service life of a smoke alarm.
by Leslie Green
 The picture shows two temperature/humidity meters of the same type, bought at the same time and from the same place. The specification in the manual that comes with the meters says that the temperature resolution is 0.1°C and the refresh rate is 10 seconds. The website selling the meters claims the accuracy is plusmn;1°C.
The picture shows two temperature/humidity meters of the same type, bought at the same time and from the same place. The specification in the manual that comes with the meters says that the temperature resolution is 0.1°C and the refresh rate is 10 seconds. The website selling the meters claims the accuracy is plusmn;1°C.
The meter on the left has been brought into the room and left to stabilise for about 2 minutes. (If it had been put on the right the reading on that meter would still have been low.)
Why are the readings so different? Which answer is the most guaranteed?
(The picture has been edited to remove branding information, and that is all.)
by Leslie Green
 The sinking of the unsinkable RMS Titanic in 1912 (after it hit an iceberg on its maiden voyage) is a well known engineering disaster story. As with many such disaster stories it was not just one thing that caused the disaster, but a whole catalog of errors.
The sinking of the unsinkable RMS Titanic in 1912 (after it hit an iceberg on its maiden voyage) is a well known engineering disaster story. As with many such disaster stories it was not just one thing that caused the disaster, but a whole catalog of errors.
The sides of the ship were 1 inch thick mild-steel plates, overlapped and hot-riveted together. In this case the iron (or steel) rivets were heated until they were red hot (actually glowing red) then pushed into holes in the steel plates and hammered over. As the rivets cooled, they contracted, making really strong joints.
We suppose that one faulty riveted joint is just about acceptable, but that two right next to each other is bad. Suppose we have 4 rivets in a row, and the probability of a faulty rivet is 1 in 1,000. Estimate the probability of two faulty rivets right next to each other.
by Leslie Green
 A manned space mission to Mars requires a reliable electrical power generation system. For this reason three of the same type of power generators are taken, each of which is sufficient to supply the requirements of the mission. The probability of failure of any one of the power systems during the flight is estimated to be 1 in 100,000.
A manned space mission to Mars requires a reliable electrical power generation system. For this reason three of the same type of power generators are taken, each of which is sufficient to supply the requirements of the mission. The probability of failure of any one of the power systems during the flight is estimated to be 1 in 100,000.
Estimate the probability of a failed mission in terms of just the electrical power supply.
by Leslie Green
 In the recycling of cars, the body of the car gets shredded by powerful machines and the resulting chunks of material first have the ferrous metal (primarily iron and steel) removed by means of permanent magnets. The next step takes the non-ferrous metals (aluminum, brass, etc) and throws these off the conveyor belt using the force from an alternating magnetic field (an eddy current separator). The non-metallic waste passes through the eddy current separator a second time to improve the separation.
In the recycling of cars, the body of the car gets shredded by powerful machines and the resulting chunks of material first have the ferrous metal (primarily iron and steel) removed by means of permanent magnets. The next step takes the non-ferrous metals (aluminum, brass, etc) and throws these off the conveyor belt using the force from an alternating magnetic field (an eddy current separator). The non-metallic waste passes through the eddy current separator a second time to improve the separation.
If we suppose that 10% of the non-ferrous material remains after the first pass, how much remains after the second pass?
by Leslie Green
 You have 4 electronic weighing scales. You test all 4 with the same 50.000kg reference weight at different times of the day, and on different days, to establish their accuracy.
You have 4 electronic weighing scales. You test all 4 with the same 50.000kg reference weight at different times of the day, and on different days, to establish their accuracy.
The results are shown below.
You want to pick the best scale to use in your new coffee bean filling station because you know that you have to supply at least as much coffee as you put on the label, but any amount more than that is just wasted as far as your profit is concerned. The bags are marked as 50kg.
Which scale should you pick?
by Leslie Green
 Leslie Green asks:
Leslie Green asks:
The image shows an electrical power meter set to read in units of kWh. Given that at the start of the test the last three digits were 9.45, and 30 minutes later the last three digits were 9.50, what was the average power consumption during that period?
(The image shows the last three digits as 9.48 as the picture was taken during the test.)
 Leslie Green asks:
Leslie Green asks:
Analyse the graph shown.
What is the strongest statement you can be sure of from this data?
Image credit: Quora
 Leslie Green asks:
Leslie Green asks:
Which material in this list is the most strongly anisotropic?
School problems often deal with uniform isotropic materials: iso- as a prefix has the sense of sameness. Isotropic materials have properties which are the same, independent of direction. The an- (or sometimes just a-) negates the following items such as anaerobic, anastigmatic.
 Leslie Green asks:
Leslie Green asks:
Consider the following statement:
"A hovering helicopter has no vertical or horizontal motion. Given that mechanical power requirement is force x velocity the mechanical power required to do so is zero so the helicopter engine is just idling when hovering."
 A certain premium digital meter has a stated DC volts accuracy specification of plusmn;[0.15% of reading + 2 counts].
A certain premium digital meter has a stated DC volts accuracy specification of plusmn;[0.15% of reading + 2 counts].
On the 6 V range it will display 6.000 V, in other words the last digit is changing in steps of 1 mV.
You have correctly set the zero reading and you are measuring a voltage of 50 mV.
What is the specified accuracy of your reading, neglecting any other considerations?
by Leslie Green
 An inexpensive hand-held laser range finder projects a red laser beam onto a wall a few meters away, and returns an accurate distance reading with 1 mm resolution.
An inexpensive hand-held laser range finder projects a red laser beam onto a wall a few meters away, and returns an accurate distance reading with 1 mm resolution.
Assuming this is a simple time-of-flight measurement of a laser pulse, what is the necessary resolution of the time measurement?
The speed of light is 3 108 m/s (300,000 km/s).
by Leslie Green
 The value of a computer depreciates evenly over five years for tax purposes (every year it is worth less by the same amount, so that it is worth $0 after five years).
The value of a computer depreciates evenly over five years for tax purposes (every year it is worth less by the same amount, so that it is worth $0 after five years).
The value of a table depreciates evenly over ten years.
If I bought the computer for $2,200 and the table for $500, how much will they be worth after 3 years?
 A group of student friends went to an open-air rock concert.
A group of student friends went to an open-air rock concert.
They evenly distributed themselves in the available cars.
Half way to the concert, two cars broke down so it was necessary for each of the remaining cars to carry one more student.
The drivers of the broken cars also went to the concert.
When they started for home town after the concert there were three persons more in each car than when they started out in the morning because two drivers individually drove to other locations.
How many students attended the concert?
 Leslie Green asks:
Leslie Green asks:
A satellite in geostationary orbit is essentially weightless. It needs to move about its axis and to nearby positions at the same orbital radius.
Which is the best (correct) statement?
 Cathy is all alone in the spaceship, 1km from the mother-ship. The (hideous) fate of the other crew members has been withheld. Cathy's spaceship is totally out of fuel and is dead in space relative to the mother-ship.
Cathy is all alone in the spaceship, 1km from the mother-ship. The (hideous) fate of the other crew members has been withheld. Cathy's spaceship is totally out of fuel and is dead in space relative to the mother-ship.
Cathy has one chance. She has created a loose bundle of equipment and waste which she estimates to be 1000kg of mass. If she can eject this mass from the airlock with enough speed she should reach the mother-ship before her air runs out. She estimates the current mass of her spaceship as 100,000kg.
Cathy cannot throw the 1000kg mass, but by pushing it and running on the ridged floor in the air-lock, she is confident she can eject the mass at 5m/s.
What is her estimate of the time to reach the mother-ship?
by Leslie Green
 John, the physics student, wishes to dry his wet rectangular towel on a radiator. He wonders how much has to overhang at the back to make the towel stable.
John, the physics student, wishes to dry his wet rectangular towel on a radiator. He wonders how much has to overhang at the back to make the towel stable.
He is reluctant to put too much of the towel behind the radiator as this is the unknown territory of stale pizza, dead bugs, cobwebs, and other indescribable debris.
He models the situation as shown, where the radiator thickness has been exaggerated. He supposes that the towel only rests against the top of the radiator, shown in red. He further supposes that the length of this red section is negligible compared to the length, L, of the towel. He guesses that the coefficient of static friction for this situation is 0.50
What is the length of the long part of the towel in the limiting case?
by Leslie Green
 By the time you have completed the calculations, and set the thrust magnitude, the 1000 kg lunar lander will be heading directly for the moon's surface at a speed of 50 m/s and just 250 m from the surface.
By the time you have completed the calculations, and set the thrust magnitude, the 1000 kg lunar lander will be heading directly for the moon's surface at a speed of 50 m/s and just 250 m from the surface.
How much thrust is needed to give a perfect landing (neglecting the weight change due to the fuel expended)?
(The gravitational acceleration on the surface of the moon is 1.6 m/s2).
by Leslie Green
 Your boss has told you to buy a more accurate (and therefore more expensive) thermocouple probe to more accurately measure the room temperature using a thermocouple meter (digital thermometer).
Your boss has told you to buy a more accurate (and therefore more expensive) thermocouple probe to more accurately measure the room temperature using a thermocouple meter (digital thermometer).
Comment on this requirement.
by Leslie Green
 Leslie Green asks:
Leslie Green asks:
The iPhone has a smooth underside resting on the smooth level surface. It has a mass of 130g. The coefficient of static friction between the phone and the surface is 0.2 exactly. I horizontally pull the phone by the attached white cable with a force of 0.2 N.
What is the magnitude of the frictional force?
1kg = 1000g
 Leslie Green asks:
Leslie Green asks:
The 0 - 60 mph (≈100 km/h) test is frequently used to compare cars. Suppose you took a car and pushed it off a cliff.
Neglecting wind resistance, how long would it take to complete this 0 to 60 mph test?
Take gravity as 10 N/kg and 60 mph as 30 m/s (it is actually 26.82 m/s, an inconvenient value for hand calculations).
 Leslie Green asks:
Leslie Green asks:
In a typical lab setup for measuring frictional force, a block (blue) is pulled by a thin string or line (green) by a weight (yellow). The pulley wheel (red) is typically considered to be free to rotate without friction in the bearing.
What is the effect of some small friction in the pulley wheel bearing?
 Your school work has finally paid off and you get to design your own electric dragster. The electric motor is so massively powerful that the torque output to the road wheels has to be limited to a certain fixed value to prevent the wheels from spinning.
Your school work has finally paid off and you get to design your own electric dragster. The electric motor is so massively powerful that the torque output to the road wheels has to be limited to a certain fixed value to prevent the wheels from spinning.
What is your prediction of the real-world performance of this new design?
by Leslie Green
 Here we show the side view of a kitchen worktop with a grain of uncooked rice (not to scale) ready to be brushed into the blue bin below.
Here we show the side view of a kitchen worktop with a grain of uncooked rice (not to scale) ready to be brushed into the blue bin below.
What is the optimal speed with which to brush the rice?
(Take the gravitational force as 10 N/kg)
by Leslie Green
 Leslie Green asks:
Leslie Green asks:
A particle has a velocity which increases in direct proportion to its distance from its origin (the zero reference point for distance).
Describe its acceleration characteristic.
 Leslie Green asks:
Leslie Green asks:
A man wishes to throw a ball such that it stays in the air for as long as possible.
The speed at which he throws the ball is some fixed value. The ground around him is featureless and level as far as the eye can see.
What is his optimum strategy?
(Neglect wind resistance and spin.)
 Leslie Green asks:
Leslie Green asks:
Nerdy McGeekface throws a baseball as hard as he can, but unfortunately hits Beefcake O'Reilly square in the back.
Neglecting any subsequent activity, who feels the most impact?
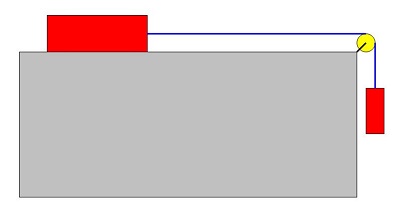 The grey block is extremely heavy and rigid, with a perfectly horizontal frictionless top surface. The blue inelastic string over the frictionless pulley transfers force without loss from the small weight to the big weight. The big weight has 3x the mass of the small weight.
The grey block is extremely heavy and rigid, with a perfectly horizontal frictionless top surface. The blue inelastic string over the frictionless pulley transfers force without loss from the small weight to the big weight. The big weight has 3x the mass of the small weight.
Initially, the masses are held in place by some unspecified device, with the string taut.
Describe the motion of the small mass when the masses are released.
Take the gravitational constant as 10N/kg.
by Leslie Green
 A toy car is released from stationary on a smooth planar slope which is angled relative to the horizontal, the sine of the angle being 0.2 (an angle of about 11.5°).
A toy car is released from stationary on a smooth planar slope which is angled relative to the horizontal, the sine of the angle being 0.2 (an angle of about 11.5°).
Taking the acceleration due to gravity as being 10m/s2, and assuming frictionless wheel bearings and negligible air resistance, describe the motion of the car (which was pointing directly downhill when released).
by Leslie Green
 Leslie Green asks:
Leslie Green asks:
Not so long ago, but before petrol engines, and before small steam engines, cargo was transported down canals in barges, pulled by horses or even people.
Why would it have been advantageous to use a long rope?
The picture shows "Barge Haulers on the Volga", an 1873 oil-on-canvas painting by the Russian artist Ilya Repin.
 Jane randomly chooses a pen from a collection of white, yellow, and cyan pens. There is an equal probability of choosing any particular color.
Jane randomly chooses a pen from a collection of white, yellow, and cyan pens. There is an equal probability of choosing any particular color.
John randomly chooses a piece of paper from a collection of white, yellow, and cyan sheets. The probability of choosing paper of a particular color is proportional to the number of sheets available. There are equal amounts of yellow and cyan, but twice as much white as yellow.
Jennifer takes the pen and paper and writes a note.
What is the probability that the writing will be visible, given that writing using a pen of the same color as the paper will not be visible?
by Leslie Green