 There are 2 different data sets.
There are 2 different data sets.
Set 1: 1, 3, 7, 9, 13, 15
Set 2: 1, 2, 7, 15, 15
Which is correct?
 Anna has 3 bags of marbles.
Anna has 3 bags of marbles.
The first contains 5 white marbles and 5 green marbles.
The second contains 2 white marbles and 8 blue marbles.
The third contains 16 white marbles and 4 green marbles.
If she randomly selects a single marble from each bag, what is the probability that all three marbles will be green?
 Tom has 3 bags of marbles.
Tom has 3 bags of marbles.
The first contains 4 white marbles and 6 green marbles.
The second contains 2 white marbles and 8 blue marbles.
The third contains 12 white marbles and 8 green marbles.
If he randomly selects a single marble from each bag, what is the probability that all three marbles will be white?
 John has an average of 89 on his three math exams.
John has an average of 89 on his three math exams.
To earn an A, he must have a 90 average.
What is the lowest grade he must earn on the next exam to raise his average to 90?
 How many different 7-digit phone numbers can be used by a phone company?
How many different 7-digit phone numbers can be used by a phone company?
The phone numbers cannot start with a zero.
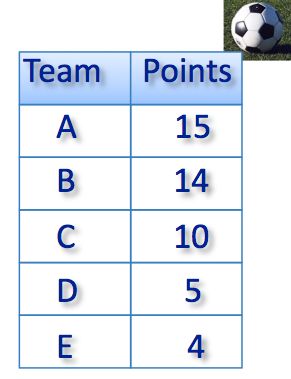 The table shows the results of a competition among 5 teams.
The table shows the results of a competition among 5 teams.
Each team plays two matches against each of the other teams, with three points for a win, one point for a draw and none for a defeat.
How many draws were there?
 As each of five eggs is weighed, the average weight increases by one gram each time.
As each of five eggs is weighed, the average weight increases by one gram each time.
If the first egg weighs 50 grams, what is the weight of the last egg?
 The probability that two randomly chosen people in a big city are younger than 25 is 25%.
The probability that two randomly chosen people in a big city are younger than 25 is 25%.
What is the probability that 3 randomly chosen people from the city are younger than 25?
 In a game, you have a 1/5 probability of winning $100 and 4/5 probability of losing $26.
In a game, you have a 1/5 probability of winning $100 and 4/5 probability of losing $26.
What is the most likely amount of money you will win (or lose) at the end of 1000 games?
 John is sick 6 days per year.
John is sick 6 days per year.
The probability of being sick on a Saturday or a Sunday is two times less than on any other day.
What is the probability that John will be sick on a Monday?
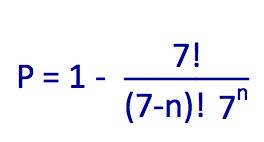 This formula, developed by Austrian mathematician Richard Von Mises, shows the probability of at least 2 people from n having their birthdays on the same day of the week.
This formula, developed by Austrian mathematician Richard Von Mises, shows the probability of at least 2 people from n having their birthdays on the same day of the week.
What is the probability that 2 people have their birthdays on the same day of the week?
 Five people sit at a round table.
Five people sit at a round table.
What is the probability that they sit in age order?
The order can be ascending or descending, clockwise or counterclockwise.
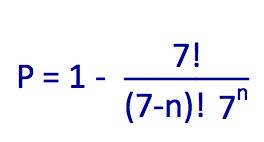 This formula, developed by Austrian mathematician Richard Von Mises, shows the probability that at least 2 people from n have their birthdays on the same day of the week.
This formula, developed by Austrian mathematician Richard Von Mises, shows the probability that at least 2 people from n have their birthdays on the same day of the week.
What is the probability that at least 2 people from 7 people have their birthdays on the same day of the week?
 A boy begins walking from his starting point. Each hour, he either walks one kilometer to the east or one kilometer to the north, but he never walks in the same direction as he did in the previous hour.
A boy begins walking from his starting point. Each hour, he either walks one kilometer to the east or one kilometer to the north, but he never walks in the same direction as he did in the previous hour.
In how many different ways can he get to a point that is 8 kilometers to the north and 8 kilometers to the east of his starting point?
 Abbey has a dog Abby.
Abbey has a dog Abby.
She places 5 tiles with the letters of her surname into a bag.
She picks up one tile after other without looking.
What word has the greatest probability of appearing in the correct order from the beginning?
 Two princes and two princesses are ready to marry.
Two princes and two princesses are ready to marry.
Everybody independently chooses a partner without telling anyone.
What is the probability that everybody chooses a person who chooses her/him?
Assuming that boys choose girls and girls choose boys.
 I randomly place three crosses into different cells of the grid.
I randomly place three crosses into different cells of the grid.
What is the probability that the crosses lie on the same straight line?
 A 4-character password uses exactly two different digits.
A 4-character password uses exactly two different digits.
Each digit can be 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9.
How many such passwords are possible?
 After a rodeo, four cowboys have a meeting in a saloon.
After a rodeo, four cowboys have a meeting in a saloon.
Each cowboy has only one bullet.
Each cowboy randomly chooses one of the other three cowboys and successfully shoots him.
What is the probability that all of them are shot?
The photograph courtesy of Roland Sauter
 Make 727 by using three 7s.
Make 727 by using three 7s.
You can use any math operator that you would like.
How many times do you use the plus sign (+) in the expression?
 Anna (A), Bill (B), Cindy (C), and Daniel (D) work on a project.
Anna (A), Bill (B), Cindy (C), and Daniel (D) work on a project.
(1) Together, A, B, and C can complete it in 10 days.
(2) Together, B, C, and D can complete it in 11 days.
(3) Together, C, D, and A can complete it in 12 days.
(4) Together, D, A, and B can complete it in 13 days.
Who is the best performer?
 A venture capitalist has choosen to invest in only one of three start-up companies: A, B, or C.
A venture capitalist has choosen to invest in only one of three start-up companies: A, B, or C.
I will make a lot of money if I invest in the same company, and will lose all of my money if I choose another company.
I decide to invest in company A and I inform the venture capitalist.
He assures me that he has not invested in company C.
What company do you recommend for me to make the investment?
 How many different cubes can I make by using six different colors such that each face has a different color?
How many different cubes can I make by using six different colors such that each face has a different color?
I can rotate the cubes.
 In a venture investment fund, all investors continue to invest into a new start-up company until the company becomes a great success.
In a venture investment fund, all investors continue to invest into a new start-up company until the company becomes a great success.
If the company fails, then the investor tries to invest into another company.
An investor stops investing if the last investment is successful.
The probability of success is 10%.
What is the total proportion of successful to failed start-up companies in the investment fund?
 What is the probability that two dominoes drawn randomly from a standard set will match (will allow concatenation)?
What is the probability that two dominoes drawn randomly from a standard set will match (will allow concatenation)?
 Tom has 3 bags of marbles.
Tom has 3 bags of marbles.
The first contains 4 white marbles and 6 green marbles.
The second contains 5 white marbles and 15 blue marbles.
The third contains 12 white marbles and 8 green marbles.
If he randomly selects a single marble from each bag, what is the probability that all three marbles will be white?
 Alex received a 90 on his essay and an 80 on his final.
Alex received a 90 on his essay and an 80 on his final.
He got a 90 on class participation.
The essay counts as 30% of his grade.
Class participation counts as 20% of his grade.
What is his grade?
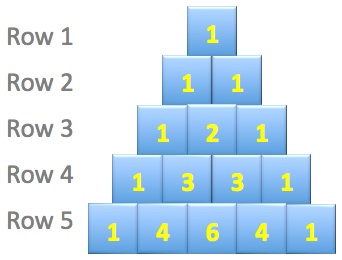 This picture shows the first five rows of Pascal's triangle.
This picture shows the first five rows of Pascal's triangle.
What is the sum of the numbers in the eleventh row of the triangle?
 What is heavier than a cumulus cloud, which is about 1 cubic kilometer in volume?
What is heavier than a cumulus cloud, which is about 1 cubic kilometer in volume?
Water is 1000 times heavier than the same volume of cloud.
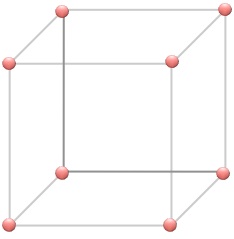 Eight bugs are at the eight corners of an equilateral cube.
Eight bugs are at the eight corners of an equilateral cube.
Each bug randomly picks a direction and moves along the edge of the cube until the next corner.
What is the probability that none of the bugs will meet another?
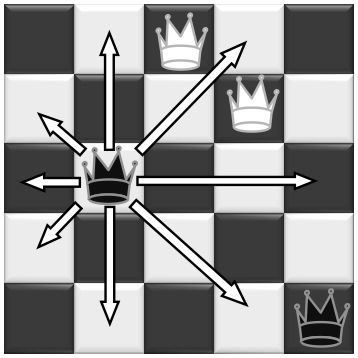 A chess queen attacks all squares along its path horizontally, vertically and diagonally.
A chess queen attacks all squares along its path horizontally, vertically and diagonally.
I would like to place at least 2 white queens and at least 2 black queens on a 5x5 chessboard, such that the queens on either side cannot attack any opposing queens.
What is the maximum number of queens I can place on the board?
 We want to merge 4 companies into one large company.
We want to merge 4 companies into one large company.
How many ways are there to merge them?
PS: you can merge only 2 companies at once.
 I want to find the smallest number divisible by 225 that consists of ones and zeros.
I want to find the smallest number divisible by 225 that consists of ones and zeros.
How many 1's are there in the number?
 Place the cards into two boxes so that the probability of randomly drawing a card with the letter B is at its maximum.
Place the cards into two boxes so that the probability of randomly drawing a card with the letter B is at its maximum.
I draw a card from a box.
What is the probability?
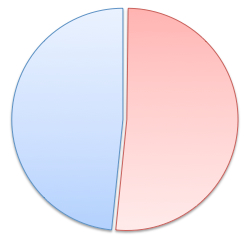 Alex possesses 52% of a business and the rest belongs to Bill.
Alex possesses 52% of a business and the rest belongs to Bill.
They take Craig into partnership so that the three partners have an equal interest in the business.
Craig pays $100,000,000.
How do Alex and Bill split the money?
 A player must match three different numbers chosen from the integers 1 to 30 in any order to win a lottery.
A player must match three different numbers chosen from the integers 1 to 30 in any order to win a lottery.
If a ticket costs $1, what is the largest possible prize so that the organizers make a profit (on average)?
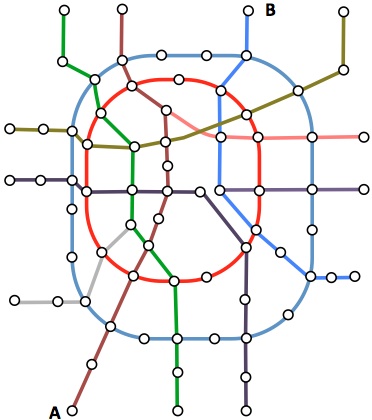 The picture shows a subway map.
The picture shows a subway map.
If it takes 3 minutes to go from one station to the next one and 3 minutes to change lines, what is minimum time required to go from A to B?
 In a country, a baby is born every 5 seconds, a person dies every 45 seconds, and a new immigrant comes to the country every 20 seconds.
In a country, a baby is born every 5 seconds, a person dies every 45 seconds, and a new immigrant comes to the country every 20 seconds.
What is the rate of growth in the country?
 This is a standard set of dominoes.
This is a standard set of dominoes.
Choose 2 dominoes at random.
What is the probability that these two dominoes match: an end of one matches at least one of the ends of the other?
 A concert includes 3 cello pieces and 3 piano pieces.
A concert includes 3 cello pieces and 3 piano pieces.
In how many ways can the program be arranged if a piano piece must come last?
 Anna and Bill roll a six-sided die.
Anna and Bill roll a six-sided die.
The first person to roll a six wins.
Anna rolls first, then Bill rolls the die.
If nobody wins, they change the order: Bill starts first and so on.
What is the ratio of Anna's and Bill chances?
 You can throw as many darts as necessary at the board shown in the picture.
You can throw as many darts as necessary at the board shown in the picture.
Some total scores are impossible to obtain, such as all the numbers less than 9 as well as 10, 12, etc.
What is the highest whole number score that is impossible to obtain?
Inspired by David Pleacher
 John threw 8 fair dimes and Mary 9 dimes.
John threw 8 fair dimes and Mary 9 dimes.
What is the probability that Mary has more heads than John?
 Estimate the total you pay if the meal costs $29, the tax is 5%, and the tip is at least 15%.
Estimate the total you pay if the meal costs $29, the tax is 5%, and the tip is at least 15%.
Round up the total.
 John and I have a glass of milk.
John and I have a glass of milk.
He drinks half of it and then I drink half of what is left.
He drinks half of what is left and I do the same.
We continue until nothing is left.
What proportion of the initial amount of the milk did I drink in total?
 Five students Anna, Bill, Craig, Daniel, and Eugene commute by bus. Every morning each student independently and randomly selects to board one of the 4 buses.
Five students Anna, Bill, Craig, Daniel, and Eugene commute by bus. Every morning each student independently and randomly selects to board one of the 4 buses.
What is the average number of students in the bus that Anna chooses?
 If the probability of observing a white car in 10 minutes on a motorway is 0.99999, what is the probability of observing a white car in 2 minutes?
If the probability of observing a white car in 10 minutes on a motorway is 0.99999, what is the probability of observing a white car in 2 minutes?
 The sum of the integers from 1 to 2,000 inclusive is 2,001,000.
The sum of the integers from 1 to 2,000 inclusive is 2,001,000.
What is the sum of the odd integers in the range?
This is a typical SAT question.
 My car can travel 20 km on one liter of gas on the motorway and 12 km on one liter of gas in the city.
My car can travel 20 km on one liter of gas on the motorway and 12 km on one liter of gas in the city.
If 60% of my travels are on the motorway, the odometer shows 15,000 km this year, and the average price is $2 per liter how much do I pay for the gas this year?
 A 512-page book weighs 800g to the nearest 10g.
A 512-page book weighs 800g to the nearest 10g.
What is the weight of 200 pages if the cover represents 20% of the book's weight?
 The sum of N consecutive integers is S.
The sum of N consecutive integers is S.
Which of the following equations gives the value of the first integer of the sequence?
 Veryfast Airlines loses 20% of the luggage.
Veryfast Airlines loses 20% of the luggage.
Gerry puts his three favorite toys in three different bags.
What is the probability that he no longer has any toys after flying with Veryfast Airlines?
 95.8% of James' classmates have different numbers of hairs than he has.
95.8% of James' classmates have different numbers of hairs than he has.
How many students are there in his class?
 A ball rebounds half of the height from which it is dropped in a sport hall.
A ball rebounds half of the height from which it is dropped in a sport hall.
It stops rebounding when the height is smaller than 2 mm (0.002 meter).
How many times does the ball rebound if it drops from your head?
 When Jane plays against Gerry in her favorite game, the odds are 5 to 3 that she will win.
When Jane plays against Gerry in her favorite game, the odds are 5 to 3 that she will win.
What is probability that she wins three games in a row?
 James the Mathematician wants to find a partner for a serious relationship. He has his own scoring system. He talks with N out of 100 girls, rejects them and records the best score S. He decides to talk to all 100 girls, making a decision about each one immediately. Once rejected, a girl cannot be recalled. After that, he continues to talk to others and stops when the girl has a score better than S.
James the Mathematician wants to find a partner for a serious relationship. He has his own scoring system. He talks with N out of 100 girls, rejects them and records the best score S. He decides to talk to all 100 girls, making a decision about each one immediately. Once rejected, a girl cannot be recalled. After that, he continues to talk to others and stops when the girl has a score better than S.
What number N do you recommend to the boy?
 Steve wonders "Why don’t I have a girlfriend?" He uses the following information. There are 10,000 girls and women who live in his city, but only 5% of them are age-appropriate for him. A total of 50% have the required level of education, and he expects that 50% of the women in the selected group are attractive to him and he hopes that at least 20% will find him attractive too.
Steve wonders "Why don’t I have a girlfriend?" He uses the following information. There are 10,000 girls and women who live in his city, but only 5% of them are age-appropriate for him. A total of 50% have the required level of education, and he expects that 50% of the women in the selected group are attractive to him and he hopes that at least 20% will find him attractive too.
How many girls in his city are potential girlfriends?
Inspired by a scientific article by Peter Backus.
 Gerry's income is seven-eighths that of Jane.
Gerry's income is seven-eighths that of Jane.
Gerry's expenses are seven-eighths those of Jane.
They spend less than they earn.
Jane promised to marry Gerry if he saves more than she does.
Who saves more money?
 The cost of living increased in the first year and it decreased in the second year by the same value.
The cost of living increased in the first year and it decreased in the second year by the same value.
What was the annual percent change if the total two-year change was minus one percent?
 I got a total of 120 by using five zeros and any mathematical operators.
I got a total of 120 by using five zeros and any mathematical operators.
How many plus signs "+" did I use?
 If you choose an answer to this question at random, what is the probability that you will be correct?
If you choose an answer to this question at random, what is the probability that you will be correct?
 I bought a 20'' (the diagonal size) laptop with the ratio of the screen width to the height 4 : 3.
I bought a 20'' (the diagonal size) laptop with the ratio of the screen width to the height 4 : 3.
How many pixels does it have if the specification declares that PPI (pixel per inch) is 200?
 I throw a coin on a chessboard.
I throw a coin on a chessboard.
The diameter of the coin is a half of the side length of a small square of the chessboard.
What is the probability that the coin touches both light and dark colors?
I don't take into account the cases when the coin touches the border of the chessboard.
 Gerry's favorite digit is 7.
Gerry's favorite digit is 7.
What is the probability that there is at least one 7 in the three-digit registration numbers of the next two cars that pass by?
 I put red and white chocolate candies into a bag.
I put red and white chocolate candies into a bag.
I randomly took 2 candies, noted their colors, and put them back into the bag.
I made 100 tests and both candies were white in 50 cases.
What is the most likely minimum possible number of candies in the bag?
 Coin landing on its edge
Coin landing on its edge
I flip a fair Swiss franc* and it falls in mousse**.
What is the probability that the coin stays on its edge after the mousse melts?
*One Swiss franc is about 1 USD; diameter 23.20mm , thickness 1.55mm, weight 4.4g.
During a coin toss, the coin is thrown into the air such that it rotates edge-over-edge several times.
**A mousse (French 'foam') is a prepared food that incorporates air bubbles to give it a light and airy texture.
 I roll two dice, one with the left hand and one with the right.
I roll two dice, one with the left hand and one with the right.
If the left hand die gives an odd number, the overall score is zero.
If the right hand die gives an even number, I roll it again and again until it is odd.
The score is the sum of the two numbers, except for the previously mentioned case.
There are exactly 6 possible scores: 0, 3, 5, 7, 9, and 11.
What is the average score?
The problem was suggested by Leslie Green
 Leslie Green asks:
Leslie Green asks:
Criminal gangs have been known to pay vagrants to search through people’s refuse to find useful information like bank statements, credit card statements, receipts and so forth. With such personal information the criminals can then pretend to be the householder and take out loans, buy things or do other bad things having stolen somebody’s identity.
Steve is fairly careful about shredding such documents, but about 5% of the time an important document slips into the refuse unshredded. Fortunately, unless he is being specifically targeted, it is pretty unlikely that somebody will be going through his refuse every week. Let’s put the odds at 1 in 1000 for each weekly collection.
Assuming that if Steve fails to shred a document, and if the criminals are searching his bins at that time, his identity will be stolen, what is the chance of that happening in a 10 year period?
 Jane was a naughty little girl. When she used to play 2-dice games with her late grandfather she always used to cheat. Her grandfather would pretend not to notice that the dice had landed and that she quickly changed one of the dice to her advantage. Specifically, if it was her throw she changed the lowest die to a 6. If it was his throw she changed the highest die to a 1.
Jane was a naughty little girl. When she used to play 2-dice games with her late grandfather she always used to cheat. Her grandfather would pretend not to notice that the dice had landed and that she quickly changed one of the dice to her advantage. Specifically, if it was her throw she changed the lowest die to a 6. If it was his throw she changed the highest die to a 1.
Over a long run of throws, how much bigger was Jane’s average score than her grandfather’s?
Author: Leslie Green
 Gerry tosses 2 coins and Jane tosses 3 coins.
Gerry tosses 2 coins and Jane tosses 3 coins.
What is the probability that Jane has more heads than Gerry does?
 There are 9 houses on a street. The distance between any two adjacent houses is the same.
There are 9 houses on a street. The distance between any two adjacent houses is the same.
There is 1 child living in house number 1, two children living in house number 2, and so on. Nine children live in house number 9.
If the school bus can only make one stop on that street, in front of which house should the bus stop so that the sum of walking distance among all children will be minimum?
 Martin has ten thousand dollars in the Mad Money's bank account. The interest rate for his account is 100% every year. The probability of the bankruptcy of the bank is 50% every year.
Martin has ten thousand dollars in the Mad Money's bank account. The interest rate for his account is 100% every year. The probability of the bankruptcy of the bank is 50% every year.
What is the expected amount of his money after three years?
 A team of two geeks, Jane and Gerry, independently answers true-or-false questions.
A team of two geeks, Jane and Gerry, independently answers true-or-false questions.
Jane answers 75% of the questions correctly, and Gerry answers 3/4 of the questions correctly.
The answer is only accepted as the team's response when the young people give the same answer.
If their answers are different, then the result is ignored.
What is the probability that a team response is correct?
 Einstein, the hyper-intelligent house cat, is busy walking from one corner of a rectangular room to the diagonally opposite corner in an apparently random manner. His rather stupid human slaves can’t work out what he is doing.
Einstein, the hyper-intelligent house cat, is busy walking from one corner of a rectangular room to the diagonally opposite corner in an apparently random manner. His rather stupid human slaves can’t work out what he is doing.
The light and dark carpet tiles on the floor look like part of a chess board, with exactly 10 tiles down the length and 6 tiles across the width. Einstein has decided to move from one corner of the room to the diagonally opposite corner, at each tile moving only down the length or across the width of the room.
How many different routes are there from one corner to the diagonally opposite corner?
[HINT: You could try an easier problem first.]
Author: Leslie Green
 Anton, the highest IQ house ant on the planet, is taking his regular nocturnal walk from one corner of the chess board (1,1) to the diagonally opposite corner (8,8), moving only right or up the board at each successive square. He remembers that on square (5,3) there is a 'black-hole', so any valid route must exclude this square.
Anton, the highest IQ house ant on the planet, is taking his regular nocturnal walk from one corner of the chess board (1,1) to the diagonally opposite corner (8,8), moving only right or up the board at each successive square. He remembers that on square (5,3) there is a 'black-hole', so any valid route must exclude this square.
From how many different paths can he choose?
[HINT: You could try an easier problem first.]
Author: Leslie Green
 Martin, the mathematical mole, has dug an extensive network of underground tunnels which he has approximated, in his magnificent mole mind, as a 3D lattice of 30 x 30 x 30 intersections. The distance between intersections is approximately constant. He is currently at intersection (20, 20, 15) and wishes to get to his secret food cache at (25, 25, 20) by one of the many shortest routes available. There are stones blocking the intersections at (21, 22, 10), (22,19,18), (22, 22, 16), (24, 18, 18) and (26, 26, 18).
Martin, the mathematical mole, has dug an extensive network of underground tunnels which he has approximated, in his magnificent mole mind, as a 3D lattice of 30 x 30 x 30 intersections. The distance between intersections is approximately constant. He is currently at intersection (20, 20, 15) and wishes to get to his secret food cache at (25, 25, 20) by one of the many shortest routes available. There are stones blocking the intersections at (21, 22, 10), (22,19,18), (22, 22, 16), (24, 18, 18) and (26, 26, 18).
From how many equally short paths can he choose?
[HINT: You could try an easier problem first.]
Author: Leslie Green
 Marek, the pan-dimensional super being, has arbitrarily defined his current location as (0,0,0,0,0,0) in 6D hyperspace. He wishes to reach location (3, 0, 2, 0, 4, 3) by one of the many shortest paths available. Despite his immense power, he can only move one hyperstep at a time, each hyperstep consisting of a unit change in exactly one of the coordinate values. Any hyperstep is of equal ‘length’.
Marek, the pan-dimensional super being, has arbitrarily defined his current location as (0,0,0,0,0,0) in 6D hyperspace. He wishes to reach location (3, 0, 2, 0, 4, 3) by one of the many shortest paths available. Despite his immense power, he can only move one hyperstep at a time, each hyperstep consisting of a unit change in exactly one of the coordinate values. Any hyperstep is of equal ‘length’.
From how many of the shortest paths can he choose?
[HINT: You could try an easier problem first.]
Author: Leslie Green
 Twenty Knights sit around the Round Table in the following order:
Twenty Knights sit around the Round Table in the following order:
1. King Arthur
2. Sir Gawain
3. Sir Lancelot
4. Sir Percival
5. Sir Galahad
6. Sir Bors
7. Sir Kay
8. Sir Gareth
9. Bedivere
10. Lucan the Butler
11. Sir Griflet
12. Sir Yvain
13. Sir Erec
14. Cador
15. Hoel
16. King Pellinor
17. Tristan
18. Morholt
19. Palemedes
20. Dinadan
Every second Knight leaves the Round Table for a battle until only one is left.
Who is he?
 Leslie Green asks: " The sinusoidal waveform shown has a peak amplitude of 20 and a period of 2. What is a rough estimate for the mean value of the waveform over the interval shown (from t=0 to t=5)? (There is no need to use Calculus).
Leslie Green asks: " The sinusoidal waveform shown has a peak amplitude of 20 and a period of 2. What is a rough estimate for the mean value of the waveform over the interval shown (from t=0 to t=5)? (There is no need to use Calculus).
HINT: Areas below the x-axis should be considered as negative when calculating the mean. "
 Christmas is getting near, and a four person company wants to run a Secret Santa scheme. The idea is that all four names are put into a hat and drawn at random. You buy a present for the person whose name you pick. Sadly, for the last three years in a row, at least one person has picked themselves, ruining the draw.
Christmas is getting near, and a four person company wants to run a Secret Santa scheme. The idea is that all four names are put into a hat and drawn at random. You buy a present for the person whose name you pick. Sadly, for the last three years in a row, at least one person has picked themselves, ruining the draw.
Estimate the probability that the draw will fail this year because somebody picks themselves.
Author: Leslie Green
 Evguenia's teacher assigns 24 math problems to solve. She sorts them from the simplest to the hardest. She can solve the simplest problem in 1 minute. Each following problem requires 2 seconds more than the previous one.
Evguenia's teacher assigns 24 math problems to solve. She sorts them from the simplest to the hardest. She can solve the simplest problem in 1 minute. Each following problem requires 2 seconds more than the previous one.
How many problems would Evguenia solve in 30 minutes?
 Five students randomly choose their places on a bench. Jane comes first and chooses a place. Any future person will only sit in a seat next to someone who is already sitting down.
Five students randomly choose their places on a bench. Jane comes first and chooses a place. Any future person will only sit in a seat next to someone who is already sitting down.
What are the chances that Gerry and Jane sit together, given that Gerry arrives last?
 John accidentally drops his text book and it falls open at a random position somewhere near the middle of the book. He immediately counts the sum of the two visible page numbers.
John accidentally drops his text book and it falls open at a random position somewhere near the middle of the book. He immediately counts the sum of the two visible page numbers.
What is the probability that the sum of the two visible page numbers is equal to the sum of three consecutive page numbers?
Author: Leslie Green
 Balls sequentially numbered from 1 to 10 are put into a box at 1 minute to noon, then number 1 is taken out. At 1/2 minute to noon balls numbered 11 to 20 are put in then number 2 is removed. At 1/3 minute to noon balls 21 to 30 are put in and number 3 is removed, and so on.
Balls sequentially numbered from 1 to 10 are put into a box at 1 minute to noon, then number 1 is taken out. At 1/2 minute to noon balls numbered 11 to 20 are put in then number 2 is removed. At 1/3 minute to noon balls 21 to 30 are put in and number 3 is removed, and so on.
How many balls are in the box at noon?
[ from A Mathematician’s Miscellany by J.E. Littlewood (1953) ]
 John takes a fair coin and tosses it until the sequence head-tail-tail (HTT) is achieved. This is one run. He records the number of tosses to achieve the result then starts again, discarding the recent coin toss history. He averages the number of tosses per run over a great many runs.
John takes a fair coin and tosses it until the sequence head-tail-tail (HTT) is achieved. This is one run. He records the number of tosses to achieve the result then starts again, discarding the recent coin toss history. He averages the number of tosses per run over a great many runs.
Mary does the same thing, but she is looking for the sequence HHH.
What can we say about the average run lengths?
[adapted from TED Global talk, July 2005, by Prof Peter Donnelly FRS]
 Anna, Bob, Cindy, and Daniel have correspondingly 50%, 60%, 70%, and 80% chances of knowing how to solve each problem correctly in the next test. They know which problem they can and cannot solve.
Anna, Bob, Cindy, and Daniel have correspondingly 50%, 60%, 70%, and 80% chances of knowing how to solve each problem correctly in the next test. They know which problem they can and cannot solve.
What average score do they expect to get if they take the test in pairs, which they wisely choose?
 In a city, all adults are married and some couples have a child. Exactly half of the population including children are in 2-member families and exactly half of the people are in 3-member families.
In a city, all adults are married and some couples have a child. Exactly half of the population including children are in 2-member families and exactly half of the people are in 3-member families.
What is the average size of a family in the city?
 I throw the dice one after another so that each throw takes me one second.
I throw the dice one after another so that each throw takes me one second.
If I will stop the game as soon as I get a 3 immediately after a 2, which follows 1, estimate the expected duration of the game.
 The Two Envelope Paradox
The Two Envelope Paradox
One envelope has twice as much money as the second one. Gerry does not know which envelope contains the larger amount.
He takes one of the envelopes, counts the money, and is offered the chance to switch the envelope.
He thinks "If the amount of money in the chosen envelope is X dollars, then the other envelope contains either 2X of 0.5X dollars, with equal probability of 0.5. The expected value of switching is 0.5 (2X) + 0.5 (0.5X) = 1.25X. This is greater than the value in the initially chosen envelope. It is better to switch."
What is your advice?
 Box A contains 3 blue balls and 1 red ball, all of the same size, weight, and texture.
Box A contains 3 blue balls and 1 red ball, all of the same size, weight, and texture.
Box B contains 1 blue ball and 2 red balls, all indistinguishable from those in box A.
I draw one ball from box A at random, examine it carefully, and put it into box B. I shake box B to mix up the balls, then draw a ball from that box at random.
What is the probability that the ball is blue?
Author: Leslie Green
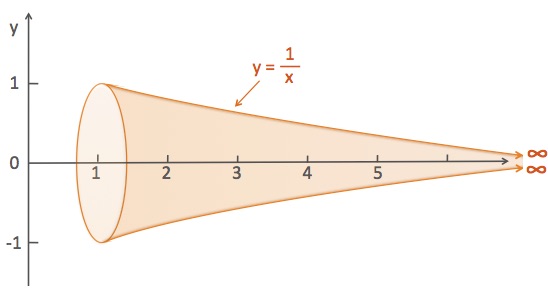 The shape obtained from rotating the equation about the x-axis resembles a trumpet. Hence, the solid so obtained is called Torricelli’s trumpet or Gabriel’s horn or the horn of infinity.
The shape obtained from rotating the equation about the x-axis resembles a trumpet. Hence, the solid so obtained is called Torricelli’s trumpet or Gabriel’s horn or the horn of infinity.
Estimate the volume and the surface area of the infinite horn.
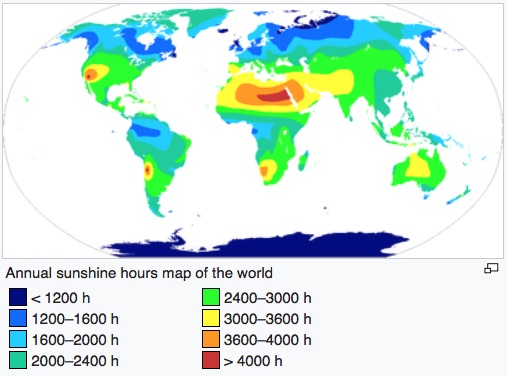 A Wikipedia article shows parts of the Earth with annual sunshine duration (sunshine hours).
A Wikipedia article shows parts of the Earth with annual sunshine duration (sunshine hours).
Estimate the percentage of the largest sunshine duration compared to the duration of an year.
 Gerry moves to an area that has floods with a 100-year recurrence interval and volcanic eruptions with 200-year recurrence interval.
Gerry moves to an area that has floods with a 100-year recurrence interval and volcanic eruptions with 200-year recurrence interval.
What is the probability of a disaster in the first year of Gerry's staying in this wonderful place?
 Leslie Green asks:
Leslie Green asks:
My black credit card has a 16-digit number. Credit cards have the digits 0-9 with equal probability in each digit position.
What is the probability that the sum of the first fifteen digits is equal to the sum of the last fifteen digits?
 There are 100 unique numbered components in a bin. You select 5 components at random. You then sort the components into numerical order.
There are 100 unique numbered components in a bin. You select 5 components at random. You then sort the components into numerical order.
How may different selections can you make (you restore the components to the bin after each selection)?
(You are specifically invited to use your calculator to solve this problem.)
Author: Leslie Green
 The picture shows problem complexity growth curves for computing problems. If N is the number of elements in the problem, then the growth can be proportional to
The picture shows problem complexity growth curves for computing problems. If N is the number of elements in the problem, then the growth can be proportional to
N2, N.log(N), N, exp(N), N! and so on.
Which type of growth is the worst (fastest)?
Author: Leslie Green
 The FastMoney bank decides to only allow passwords with a length of exactly 8 characters. Each position in the password can contain a lower case letter, an upper case letter, a digit, or a special character. For simplicity we will take the sum as 70 possible characters per position.
The FastMoney bank decides to only allow passwords with a length of exactly 8 characters. Each position in the password can contain a lower case letter, an upper case letter, a digit, or a special character. For simplicity we will take the sum as 70 possible characters per position.
The bank then randomly asks for the character in 4 unique positions within the password. For example on one day it might ask for characters in positions 3, 6, 2, and 5.
Assuming that you have chosen to not repeat any character within your password, how many unique key sequences are possible for you to correctly logon to your existing account.
Author: Leslie Green
 Your boss has asked you to produce a report of average sales figures over the last few years.
Your boss has asked you to produce a report of average sales figures over the last few years.
What rule should you use to calculate the average value?
Author: Leslie Green
 How many integers have at least one non-trivial factor under 10?
How many integers have at least one non-trivial factor under 10?
(plusmn;1 are trivial factors of any integer, as is plusmn; the number itself.)
Inspired by Vincent Granville
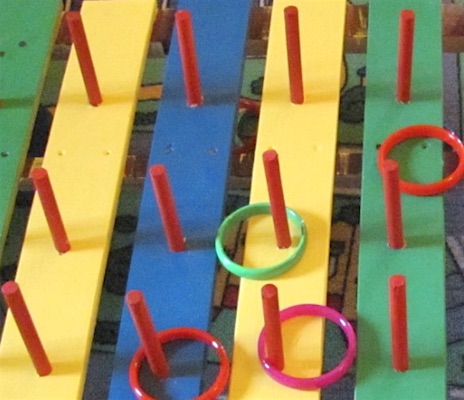 In a typical carnival game, the player tries to throw a rubber ring over a wooden peg.
In a typical carnival game, the player tries to throw a rubber ring over a wooden peg.
We won't consider any "tricks of the trade" which reduce the player's chance of winning. Consider the ring falling straight down onto the pegs at random.
Call the peg diameter P, with the inner diameter of the ring as 2P. The pegs are on a square grid of 5P side length and large extent (lots of pegs).
The outer diameter of the ring is small and doesn't affect the outcome.
Success is defined as those cases where the ring falls directly over the peg without hitting it first.
What is the probability of random success?
Author: Leslie Green
 Alan, aged 10, has a devious plan to "prove" that he is good at mathematics. He plans to go on to the site ApusClick.com and take on questions for 17 year olds in front of a single adult witness. He will randomly click on answers to two questions only. If he gets both correct he gets his witness to tell everyone what happened, "proving" his brilliance. If he gets any question wrong, he immediately stops, discards that adult, and picks a new witness.
Alan, aged 10, has a devious plan to "prove" that he is good at mathematics. He plans to go on to the site ApusClick.com and take on questions for 17 year olds in front of a single adult witness. He will randomly click on answers to two questions only. If he gets both correct he gets his witness to tell everyone what happened, "proving" his brilliance. If he gets any question wrong, he immediately stops, discards that adult, and picks a new witness.
Alan is especially lazy, and can't even be bothered to remember what the correct answer is when he has answered a question previously.
What is the probability of Alan proving his brilliance if he has a pool of 20 adults to use?
(Please use a calculator if you need to.)
Author: Leslie Green
 Suppose you want to photograph the cat when it passes through an invisible beam, but you also want to know where it came from. You automatically record the digital camera images to a memory buffer, one after the other, always overwriting the oldest image. The buffer has a certain length, and when you get to the end, you start again at the beginning. Each position in the buffer has a positive index, starting from 0. You write to the current position, then increase the position counter by one. When you increase beyond the end of the buffer you reset the counter to zero.
Suppose you want to photograph the cat when it passes through an invisible beam, but you also want to know where it came from. You automatically record the digital camera images to a memory buffer, one after the other, always overwriting the oldest image. The buffer has a certain length, and when you get to the end, you start again at the beginning. Each position in the buffer has a positive index, starting from 0. You write to the current position, then increase the position counter by one. When you increase beyond the end of the buffer you reset the counter to zero.
The position counter is called POS. The buffer length is called BLENGTH.
What is the correct value for the position counter if you want to go back 20 images from the last image?
Author: Leslie Green
 Jane is studying the subject of fluid mechanics from text books. In the first book she reads she estimates that there were 1000 key facts presented. In the next book she reads this also presents 1000 facts, but half of these are duplicates of what she has already read, but more worryingly, 0.1% contradict previous facts.
Jane is studying the subject of fluid mechanics from text books. In the first book she reads she estimates that there were 1000 key facts presented. In the next book she reads this also presents 1000 facts, but half of these are duplicates of what she has already read, but more worryingly, 0.1% contradict previous facts.
If every future book she reads has 1000 facts, but new facts halve in number with each successive book, and contradictions occur randomly at a fixed 0.1% rate, what is her projected accumulation of true facts after she has studied an infinite number of such books?
Author: Leslie Green
 I have put 3 ordinary 6 sided dice in a cup, and I am shaking them. Before I cast them out onto a table I want you to decide, using the mystical powers of your mind.
I have put 3 ordinary 6 sided dice in a cup, and I am shaking them. Before I cast them out onto a table I want you to decide, using the mystical powers of your mind.
If you win you get to pick a prize from the prize table. Otherwise you will get nothing.
Author: Leslie Green
 Jane and Gerry put the marbles in a bag.
Jane and Gerry put the marbles in a bag.
Without looking, Jane takes two marbles, then Gerry takes one.
What are the chances for him getting the red marble?
 Jane and Gerry put the marbles in a bag.
Jane and Gerry put the marbles in a bag.
Without looking, Jane takes eleven marbles one by one, then Gerry takes the last one.
What are the chances for him getting the red marble?
 Medical Test.
Medical Test.
A particular test for a disease is 96% accurate.
If one has the disease, the test comes back 'Yes' 96% of the time, and if one does not have the disease, the test comes back 'Yes' 4% of the time.
If 100 of 10000 tested patients have the disease, what is the probability that the person with the diagnosis 'Yes' has the disease?
 There are 4 transparent and 11 green-glass soda bottles in a crate.
There are 4 transparent and 11 green-glass soda bottles in a crate.
In how many different ways can the bottles be arranged in the crate?
 Ten bees work today. Each bee, after the first one, collects one less than twice as many grains of pollen as the previous bee.
Ten bees work today. Each bee, after the first one, collects one less than twice as many grains of pollen as the previous bee.
If the first bee has 2 grains of pollen, how many grains did the last bee collect?
 Gerry aims at the center (centre) of the large target. He is sufficiently accurate that he always hits the target. He throws 2 darts and adds up the scores.
Gerry aims at the center (centre) of the large target. He is sufficiently accurate that he always hits the target. He throws 2 darts and adds up the scores.
What is his chance to score 2 in total?
 Compare the security of a 4 digit passcode using two different entry methods:
Compare the security of a 4 digit passcode using two different entry methods:
In the first method all 4 digits are entered and an ENTER button is pressed.
In the second method each digit is ENTER'ed in turn, and the next digit can only be entered once the previous digit has been validated.
Consider only the unlucky (worst) case for each method.
What is the ratio of the number of ENTER key presses of the first method compared to the second method?
Author: Leslie Green
 At a factory, a quality controller inspects 5 randomly-selected light sets out of every 800 items produced.
At a factory, a quality controller inspects 5 randomly-selected light sets out of every 800 items produced.
At this rate, how many
sets are inspected every year if the factory produces 500,000 lights annually?
This is typical SAT question.
 Martin had $100 million three years ago.
Martin had $100 million three years ago.
He had $120 million two years ago.
He had $144 million last year.
How much money does he expect to have at the end of this year?
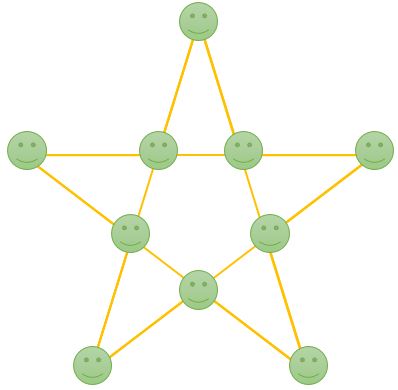 Ten brave men are in the corners of a pathway that has the shape of a regular star.
Ten brave men are in the corners of a pathway that has the shape of a regular star.
At the same moment in time, each of them randomly chooses a direction and starts walking.
Estimate the probability that nobody meets another man?
 You have two pairs of socks.
You have two pairs of socks.
You blindly choose two of four.
How much greater is the probability of getting a mismatched pair compared to a matched pair?
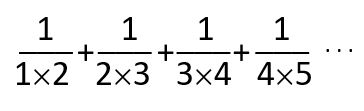 Find the sum.
Find the sum.
In 1802, Cambridge University, UK asked this problem to students seeking a bachelor’s degree.
 The probability of meeting a bear in a 3-day hiking trip in the Wild Life National Park is 0.875.
The probability of meeting a bear in a 3-day hiking trip in the Wild Life National Park is 0.875.
What is the probability of meeting a bear in an 1-day hiking trip?
 One of the most ancient examples of literature on clay tablets says that Gilgamesh was 1/3 god and 2/3 human.
One of the most ancient examples of literature on clay tablets says that Gilgamesh was 1/3 god and 2/3 human.
How many generations before his birth were the ancestors of Gilgamesh pure humans and gods?
If Gilgamesh existed, he probably was a king who reigned a kingdom in Mesopotamia sometime between 2800 and 2500 BC.
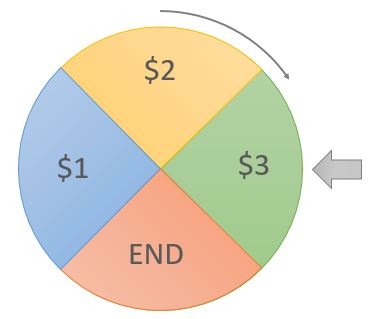 Leslie Green asks:
Leslie Green asks:
You spin a wheel and it randomly lands on $1, $2, $3, or END. If you land on $1, $2, or $3 you get that money and spin the wheel again. You keep receiving money until you land on END.
What is the probability of receiving $2 or more when playing this game once?
 Consider an extremely rare event which might randomly happen with a probability, P, of 1 in 1 million million (10-12). This might be the probability of your street getting hit by a meteorite during a particular hour, for example, but we don't pretend for an instant that the probability given is actually correct for such an event. Now consider that this event has 10 million chances to occur (N), so for our example we might say our observation period was 10 million hours.
Consider an extremely rare event which might randomly happen with a probability, P, of 1 in 1 million million (10-12). This might be the probability of your street getting hit by a meteorite during a particular hour, for example, but we don't pretend for an instant that the probability given is actually correct for such an event. Now consider that this event has 10 million chances to occur (N), so for our example we might say our observation period was 10 million hours.
How should you calculate the chance that the event will occur within the stated interval when using a handheld calculator?
Author: Leslie Green
 The black washer is constrained to randomly fall flat onto the outer square, the outer edge of the washer being within the outer square. The diagram is exactly to scale.
The black washer is constrained to randomly fall flat onto the outer square, the outer edge of the washer being within the outer square. The diagram is exactly to scale.
What is the probability that we see only red through the hole in the washer?
by Leslie Green
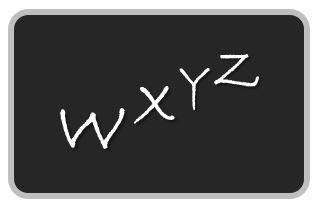 The numbers W, X, Y, and Z are 1, 2, 3, and 4 in some order.
The numbers W, X, Y, and Z are 1, 2, 3, and 4 in some order.
What is the order of the numbers to get the greatest possible value of the expression on the black board?
![]() The manufacturer of a 5000 point linear sensor array for flatbed scanners has a new quality manager. The old quality manager ignored single isolated pixel faults within the array, but rejected an array where two faulty pixels were right next to each other. The new quality manager wishes to improve quality by rejecting dual-fault arrays if the two pixels are within 10 pixels of each other.
The manufacturer of a 5000 point linear sensor array for flatbed scanners has a new quality manager. The old quality manager ignored single isolated pixel faults within the array, but rejected an array where two faulty pixels were right next to each other. The new quality manager wishes to improve quality by rejecting dual-fault arrays if the two pixels are within 10 pixels of each other.
Pixel faults are entirely random, and occur with a probability P = 10-5 (1 in 100,000).
To be clear about this, the pixels are all in a single straight line. If pixels 1 and 11 are faulty, that is the limiting case of a faulty array.
Considering only two-fault arrays, how much more probable is a failed array under the new scheme?
If you don't know where to start with this problem, try an easier one first.
by Leslie Green
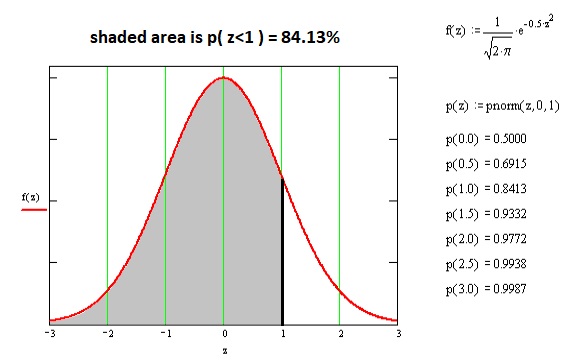 You have been told that the weight of cabbages produced by the hydroponics facility has a Gaussian (Normal) distribution with a mean of 1000g and a standard deviation of 100g. Estimate the proportion of cabbages in the range 900g to 1100g.
You have been told that the weight of cabbages produced by the hydroponics facility has a Gaussian (Normal) distribution with a mean of 1000g and a standard deviation of 100g. Estimate the proportion of cabbages in the range 900g to 1100g.
by Leslie Green
 You are in charge of quality control in a factory producing tens of thousands of self-sealing stem bolts per day. You measure the length of every bolt and produce a statistics report for the management every month. You have curve-fitted the data to a Gaussian (Normal) distribution and extracted the mean and variance data.
You are in charge of quality control in a factory producing tens of thousands of self-sealing stem bolts per day. You measure the length of every bolt and produce a statistics report for the management every month. You have curve-fitted the data to a Gaussian (Normal) distribution and extracted the mean and variance data.
Is it correct to calculate the out-of-tolerance rate using statistical tables based on the measured mean and variance data?
by Leslie Green
 Leslie Green asks:
Leslie Green asks:
Multiplication of 2 x 2 matrices is boring and only for little kids ... except perhaps when they contain imaginary numbers.
i is the square root of minus one.
What is the value of X?
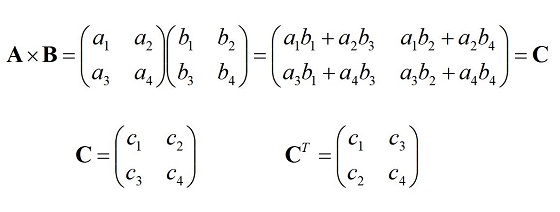 The transpose of a matrix is constructed by interchanging rows with columns. Such a matrix is identified by a superscript T.
The transpose of a matrix is constructed by interchanging rows with columns. Such a matrix is identified by a superscript T.
If a matrix is equal to its own transpose, what is a necessary and sufficient description?
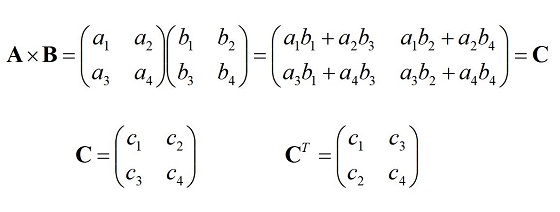 Matrix multiplication in general is non-commutative.
Matrix multiplication in general is non-commutative.
For ordinary numbers (real and integer) and even for complex numbers, multiplication is commutative. You can swap the order and get the same result.
Here we show the multiplication of two general 2 x 2 matrices, producing a third 2 x 2 matrix.
What is the result of B x A?
 What is the fewest number of people that could have visited a movie show in the open-air cinema, if exactly 99.84% of the people watched the film until the end?
What is the fewest number of people that could have visited a movie show in the open-air cinema, if exactly 99.84% of the people watched the film until the end?
 Leslie Green asks:
Leslie Green asks:
Now that John has to handle his own laundry, he has invented a new scheme. The top pullover on the shelf is the next one he wears. After washing, the cleaned and dried pullovers are placed back on top of the pile.
What is the best name for such a system?
 Patricia randomly chooses a pen from a large collection of white, yellow, and blue pens. The numbers of white and yellow pens are the same. There are twice as many blue pens as white pens.
Patricia randomly chooses a pen from a large collection of white, yellow, and blue pens. The numbers of white and yellow pens are the same. There are twice as many blue pens as white pens.
Peter randomly chooses a piece of paper from a large collection of white, yellow, and blue sheets. There are equal amounts of yellow paper and blue paper, but twice as much white as yellow.
Wendy takes the pen and paper and writes a note.
What is the probability that the writing will not be visible? (This occurs when the pen and paper are the same color.)
by Leslie Green