 Mr. Smith can read 1 page in 2 minutes. His wife can read 2 pages in 1 minute.
Mr. Smith can read 1 page in 2 minutes. His wife can read 2 pages in 1 minute.
Reading together two different books, how many minutes will it take them to read 55 pages?
 Mr. Smith can read 1 page in 2 minutes. His wife can read 2 pages in 1 minute.
Mr. Smith can read 1 page in 2 minutes. His wife can read 2 pages in 1 minute.
Reading together two different books, how many minutes will it take them to read 55 pages?
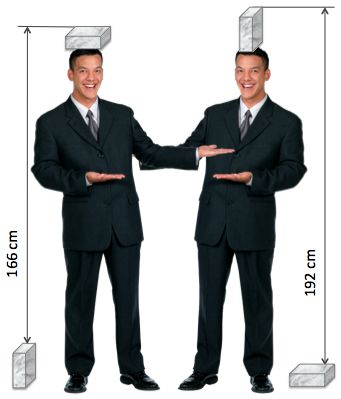 The twins are the same height.
The twins are the same height.
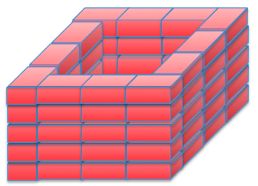
They place four identical blocks as shown in the figure.
How tall are the boys?
 Ten years ago, Bob was three times as old as Anna.
Ten years ago, Bob was three times as old as Anna.
Today, he is twice as old as Anna.
How old is Bob today?
 Statement 1: There are 3 animals in a room.
Statement 1: There are 3 animals in a room.
Statement 2: All of the animals in the room are kittens.
Question: How many legs are there in the room?
What is sufficient to answer the question?
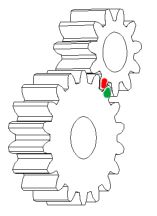 Two gears, one with 11 teeth and the other one with 18 teeth, have teeth marked as indicated.
Two gears, one with 11 teeth and the other one with 18 teeth, have teeth marked as indicated.
After how many rotations of the small gear will the marked teeth be in the same position again for the first time?
 1. At least 1 of these 6 statements is false
1. At least 1 of these 6 statements is false
2. At least 2 of these 6 statements are false
3. At least 3 of these 6 statements are false
4. At least 4 of these 6 statements are false
5. At least 5 of these 6 statements are false
6. At least 6 of these 6 statements are false
How many sentences are true?
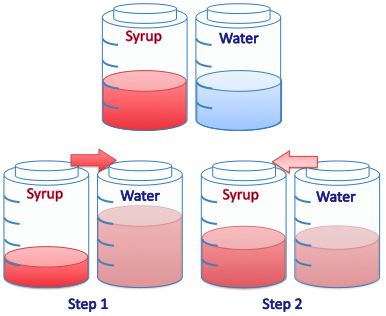 You take half of the syrup and mix it with the water, and then take the same quantity from the water jar and mix it with the syrup.
You take half of the syrup and mix it with the water, and then take the same quantity from the water jar and mix it with the syrup.
Does the syrup now contain more water than the water does syrup, or the other way round?
 A hunter met two shepherds, one of whom had three loaves of bread and the other, five loaves. All the loaves were the same size. The three men agreed to share the eight loaves equally between them. After they had eaten, the hunter gave the shepherds eight bronze coins as payment for his meal.
A hunter met two shepherds, one of whom had three loaves of bread and the other, five loaves. All the loaves were the same size. The three men agreed to share the eight loaves equally between them. After they had eaten, the hunter gave the shepherds eight bronze coins as payment for his meal.
How should the two shepherds fairly divide this money?
Paul Sloane, Lateral Thinking Puzzles, 1991
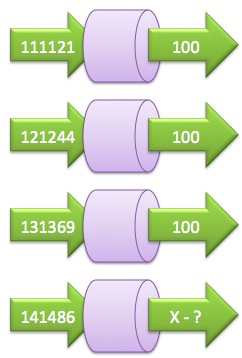 In-Out Machine transforms 111121 into 100.
In-Out Machine transforms 111121 into 100.
The same machine transforms 121244 into 100.
The same machine transforms 131369 into 100.
Find the result of the transformation, if the input is 141486.
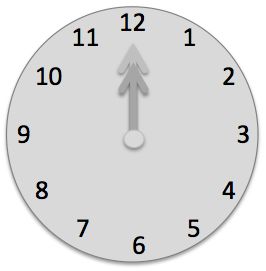 An analog clock loses 15 minutes each hour.
An analog clock loses 15 minutes each hour.
If the clock is set correctly at noon, what time is shown when it first reads the correct time again?
 Sixteen European teams enter a football tournament.
Sixteen European teams enter a football tournament.
Each team plays one match against each of the other teams, with three points for a win, one point for a draw and none for a defeat.
The probability of a draw is 0.5.
What is the most likely score of a team?
 A lady, attempting to avoid revealing her real age to her husband, says:
A lady, attempting to avoid revealing her real age to her husband, says:
I'm twenty-two years old if you do not count weekends and one summer month of every year.
Guess her real age.
 The addition shown here has 21 terms and the last element consists of 21 9's.
The addition shown here has 21 terms and the last element consists of 21 9's.
Find the three last digits of the sum.
 I put $990 into 10 envelopes.
I put $990 into 10 envelopes.
I try to compose all possible whole amounts from $1 to $990 by giving you a certain number of these envelopes.
What is the minimum amount that cannot be composed by a set of these envelopes?
 If 12 workers take 7 hours to build a brick wall 21 m long and 4 m high, how long will it take 11 workers to build a brick wall 1 m longer and 1 m higher?
If 12 workers take 7 hours to build a brick wall 21 m long and 4 m high, how long will it take 11 workers to build a brick wall 1 m longer and 1 m higher?
 Alex has bills of different dollar values.
Alex has bills of different dollar values.
There are five times as many ones as there are fives.
There are ten times as many ones as there are tens.
There are twice as many tens as there are twenties.
How much money does he have?
Find the minimum possible value.
 On January 1st, Anna and Bill have $100 each.
On January 1st, Anna and Bill have $100 each.
Each month Anna saves $10 more than she spends while Bill spends $5 more than he saves.
At the beginning of what month is Anna 10 times richer than Bill?
 Four painters can complete a painting job in 20 days.
Four painters can complete a painting job in 20 days.
12 more painters join the team 4 days after starting work on the job.
How many days does the painting job take from start to finish?
 Anna bought 1 slice of mushroom pizza and 2 slices of cheese pizza for a total of $3.
Anna bought 1 slice of mushroom pizza and 2 slices of cheese pizza for a total of $3.
Bill bought 4 slices of mushroom pizza and 5 slices of cheese pizza for a total of $9.
What is the cost of one slice of mushroom pizza?
 Twelve couples met at a party.
Twelve couples met at a party.
Each person shook the hand of each of the other people except their beloved spouse.
How many handshakes were there?
 There are a number of apples, all of different weights.
There are a number of apples, all of different weights.
The 10 lightest apples weigh 40% of the total weight.
The 5 heaviest apples weigh 25% of the total weight.
How many apples are there?
 John has just had a 1% net pay rise.
John has just had a 1% net pay rise.
He used to take home $5,000 a month.
He told his wife that the rise was a third of a percent.
How much more money does he keep for personal spending this year?
 Which of these diagrams could be drawn without taking the pen off the page and without drawing along a line twice?
Which of these diagrams could be drawn without taking the pen off the page and without drawing along a line twice?
 Each of these seven cells contains one number from 1 to 7, using all seven numbers.
Each of these seven cells contains one number from 1 to 7, using all seven numbers.
The sum of the four horizontal cells is 16.
The sum of four vertical cells is 17.
What is the number in the shared, corner cell?
 You have four piles: three piles with real coins and one pile with fake coins.
You have four piles: three piles with real coins and one pile with fake coins.
All the real coins weigh 20 grams each, and the fake coins weigh 21 grams.
How many times do you need to use a digital kitchen scale to find the pile with the fake coins?
 Use each digit, 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9, exactly once to form two 5-digit numbers that when multiplied produce the largest quantity.
Use each digit, 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9, exactly once to form two 5-digit numbers that when multiplied produce the largest quantity.
Which is the larger of the two numbers?
Source: Mathematics Teacher, NCTM Journal
 A bee crawls along the sides of the honeycomb hexagons.
A bee crawls along the sides of the honeycomb hexagons.
It has moved from point A to point B along the shortest possible path.
It can move in three different directions and made an even number of steps.
What statement is correct?
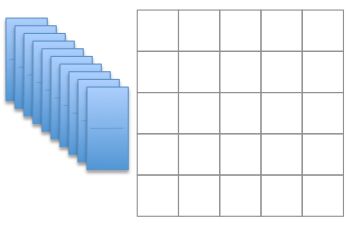 On a 5 × 5 grid, I place a 1x2 card so that it exactly covers two squares.
On a 5 × 5 grid, I place a 1x2 card so that it exactly covers two squares.
I continue until there is no place for a card.
There is no card overlapping and all cards are inside the grid.
What is largest number of empty squares I can leave at the end of the exercise?
 One hundred and thirty shareholders decide to buy 30,000 shares of company A.
One hundred and thirty shareholders decide to buy 30,000 shares of company A.
They decide that five gentlemen together will buy a thousand shares, and that four ladies together will buy a thousand shares.
How many gentlemen are there?
 A project manager has to determine whether to purchase or rent four cars for a construction project. The car is available at a rental fee of $900 per day. Purchasing the cars costs $140,000 for the investment and $100 for the daily cost.
A project manager has to determine whether to purchase or rent four cars for a construction project. The car is available at a rental fee of $900 per day. Purchasing the cars costs $140,000 for the investment and $100 for the daily cost.
After how many days would the cost of renting and purchasing the cars be equal?
 I want to measure exactly six minutes from the moment I touch an hourglass, using only a five-minute hourglass and a four-minute hourglass.
I want to measure exactly six minutes from the moment I touch an hourglass, using only a five-minute hourglass and a four-minute hourglass.
How many times do I flip over an hourglass?
Count the initial flip(s) and find the minimum possible number.
 Logic puzzle: a secret door.
Logic puzzle: a secret door.
A man approached the door of a secret laboratory and the door robot said "SIX." The man replied, "THREE" and was let in.
Another day, the robot said, "TWELVE."
The man replied, "SIX" and was let in.
Today, the robot said, "FOURTEEN."
What should the man say?
 One hundred soldiers form a 10 x 10 square.
One hundred soldiers form a 10 x 10 square.
From every column, the tallest soldier is chosen, and from these 10 soldiers, the shortest is chosen. His height is X.
At the same time, the shortest soldier is chosen from every row, and from these 10 soldiers, the tallest is chosen. His height is Y.
Compare the heights.
 A donkey must transport 900 carrots to the market, which is 300 miles away.
A donkey must transport 900 carrots to the market, which is 300 miles away.
The donkey carries a maximum of 300 carrots, and eats 1 carrot every mile.
What is the largest number of carrots that can be delivered at the market?
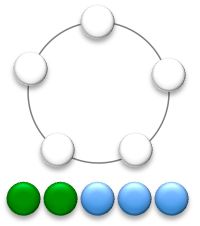 I arrange five marbles randomly in a ring.
I arrange five marbles randomly in a ring.
There are two green and three blue marbles.
What is the probability that all blue marbles are adjacent?
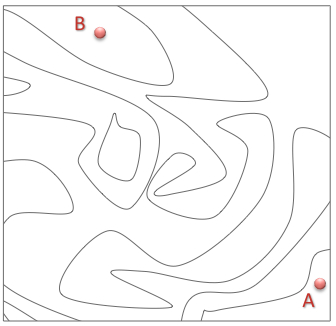 You have a part of a black-and-white map of a reef coast.
You have a part of a black-and-white map of a reef coast.
You are at point A on the coast, while a treasure is at point B.
Is the treasure under water?
 In any 24-hour period, how many times are the digits of a 24-hour digital clock in an increasing gapless counting sequence, eg 3:45?
In any 24-hour period, how many times are the digits of a 24-hour digital clock in an increasing gapless counting sequence, eg 3:45?
 Alex greeted Bill.
Alex greeted Bill.
Bill greeted Cindy.
Alex did not greet Cindy.
If the first two statements are true, the last one is:
 Kevin cleans rooms in a student hostel; he earns twice as much for cleaning a large room as he does for cleaning a small room. Yesterday he cleaned five large rooms and three small ones. If, instead, he had cleaned three large rooms and five small rooms, he would have earned $10 less.
Kevin cleans rooms in a student hostel; he earns twice as much for cleaning a large room as he does for cleaning a small room. Yesterday he cleaned five large rooms and three small ones. If, instead, he had cleaned three large rooms and five small rooms, he would have earned $10 less.
How much does he earn for cleaning a small room?
 After a three-hour drive, I stopped my car in front of a wall with three doors: a silver door on the left, a gold door in the middle, and an iron door on the right. Which door would I open first?
After a three-hour drive, I stopped my car in front of a wall with three doors: a silver door on the left, a gold door in the middle, and an iron door on the right. Which door would I open first?
 Divide the circles into two disjoint groups so that the sums of the numbers in each group are equal.
Divide the circles into two disjoint groups so that the sums of the numbers in each group are equal.
What is the sum?
 I drive to my country house at a constant speed of 100 miles/hour.
I drive to my country house at a constant speed of 100 miles/hour.
I immediately turn and drive back at another constant speed.
The entire journey takes one hour and the distance to my country house is 40 miles.
What was my speed on the back way?
 Anna, Beatrice, and Cindy run a 2000-meter race.
Anna, Beatrice, and Cindy run a 2000-meter race.
All of them run at a constant speed.
Anna beats Beatrice by 100 meters.
Beatrice beats Cindy by 100 meters.
By how many meters does Anna beat Cindy?
 Bob earns $48,000 per year and has two weeks of paid vacation.
Bob earns $48,000 per year and has two weeks of paid vacation.
He works five days a week and eight hours a day.
What is his hourly wage?
 "Three sailors come across a pile of coconuts. The first sailor takes half of them plus half a coconut. The second sailor takes half of what is left, plus half a coconut. The third sailor also takes half of what remains, plus half a coconut. Left over is exactly one coconut, which they toss to a monkey.
"Three sailors come across a pile of coconuts. The first sailor takes half of them plus half a coconut. The second sailor takes half of what is left, plus half a coconut. The third sailor also takes half of what remains, plus half a coconut. Left over is exactly one coconut, which they toss to a monkey.
How many coconuts were in the original pile?"
Martin Gardner
 There are 12 people in a village.
There are 12 people in a village.
They consume 12 coconuts altogether.
Each man eats two coconuts, each woman eats a half, and each child eats a quarter.
How many men are there?
 Vladimir Arnold (1937-2010), one of the greatest 20th century Russian mathematicians told the following story:
Vladimir Arnold (1937-2010), one of the greatest 20th century Russian mathematicians told the following story:
“Our schoolteacher, I. V. Morozkin, gave us the following problem:
Two old women started at sunrise and each walked at a constant (different) velocity. One went from A to B and the other from B to A. They met at noon and, continuing with no stop, arrived respectively at B at 4 p.m. and at A at 9 p.m.
At what time was the sunrise on this day?"
 A committee consists of 7 people. The committee keeps an important object in a safe.
A committee consists of 7 people. The committee keeps an important object in a safe.
How many mechanical locks must the safe have so that it can be opened precisely when at least 4 members of the committee are present?
You may suggest your design of the lock(s).
 Mr. Rapid always starts driving on a road at exactly 7:00 a.m.
Mr. Rapid always starts driving on a road at exactly 7:00 a.m.
If he drives on cruise control at 42 miles per hour, he arrives at work late.
If he sets the cruise control to 48 miles per hour, he arrives at work early.
The amount of time he is early is also the amount of time he is late.
How fast should he go to get to his office exactly on time?
 On an island, three-quarters of the men are married to four-fifths of the women.
On an island, three-quarters of the men are married to four-fifths of the women.
What is the minimum possible number of people on the island?
 Working alone, Mr. Smith earns the family's monthly budget in 40 calendar days.
Working alone, Mr. Smith earns the family's monthly budget in 40 calendar days.
Working alone, his beloved wife earns the budget in 2 months.
How long will it take the family to earn an additional monthly budget?
 The rear tires of a car wear out after 40,000 miles, while the front tires wear out after 50,000 miles.
The rear tires of a car wear out after 40,000 miles, while the front tires wear out after 50,000 miles.
Estimate how many miles the car can drive if I change the tires (front - rear) at the best moment.
 There are 123 part-time employees and 321 full-time employees in a company.
There are 123 part-time employees and 321 full-time employees in a company.
If the part-time employees switch from 60% occupation to 40%, how many of them can be hired for a full-time position?
 Students at a school are on average 165 cm tall.
Students at a school are on average 165 cm tall.
The average male student height is 172 cm and the average female student height is 160 cm.
What is the ratio of boys to girls in the school?
 Mary can complete an activity in 40 days.
Mary can complete an activity in 40 days.
John can complete the activity in 50 days.
Estimate for how many days they work on two activities if they change them at the best moment.
 How many uninteresting numbers exist?
How many uninteresting numbers exist?
The question is based on the interesting number paradox, which is a semi-humorous paradox, which arises from the attempt to classify natural numbers as "interesting" or "dull."
 A 44-month long project is divided into three consecutive activities.
A 44-month long project is divided into three consecutive activities.
The time between the midpoints of the first and last activities is 33 months.
What is duration of the middle activity?
 Sixteen teams enter a football tournament.
Sixteen teams enter a football tournament.
Each team plays one match against each of the other teams, with three points for a win, one point for a draw and none for a defeat.
How many games does our team lose if it scores 20 points and wins 3 games?
 "This is a capital letter of the alphabet that's been folded just once.
"This is a capital letter of the alphabet that's been folded just once.
Which letter is it if I unfold it? "
The puzzle was created by puzzlemaster Scott Kim
 Two trains are 1 kilometer apart on a single track railway line. They set off towards one another at 1 m/second.
Two trains are 1 kilometer apart on a single track railway line. They set off towards one another at 1 m/second.
A bee sitting on the front of one of the trains sets off and starts to fly along the railway line at 3 m/second.
When the bee meets the other train it immediately turns around and flies towards the first train and so on . . .
How many times does the bee turn before the trains bump into each other?
 If each coconut is priced at $9, then the shopkeeper loses $11.
If each coconut is priced at $9, then the shopkeeper loses $11.
If each coconut is priced at $11, then the shopkeeper gains a profit of $9.
How many coconuts are there?
 Two successive increases of 25% and 25% are followed by two successive discounts of 25% and 25%.
Two successive increases of 25% and 25% are followed by two successive discounts of 25% and 25%.
What percentage is the result?
 If Gerry gives Jane one apple, they will have the same number of apples.
If Gerry gives Jane one apple, they will have the same number of apples.
If Jane gives Gerry one apple, he will have twice as many apples as she has.
How many apples do they have?
Gerry is a gentleman and so always gives Jane apples.
 At the end of each week, Gerry forgot 50% of what he knew the week before.
At the end of each week, Gerry forgot 50% of what he knew the week before.
At the end of which week Gerry knew less than 50% of all he studied?
 After an hour, Evguenia catches and frees 10 fish.
After an hour, Evguenia catches and frees 10 fish.
If there are 100 fish in a lake how many fish remain uncaught after 5 hours?
 I choose a 4-digit number in which the first digit is one-sixth the last, and the second and third digits are the last digit multiplied by 6.
I choose a 4-digit number in which the first digit is one-sixth the last, and the second and third digits are the last digit multiplied by 6.
What is the sum of all digits?
 A grandmother prepared bowls of fruit for her family. The only fruits available to her were cherries, apricots and red currants. Of course no bowl was empty and each bowl contained one kind of fruit.
A grandmother prepared bowls of fruit for her family. The only fruits available to her were cherries, apricots and red currants. Of course no bowl was empty and each bowl contained one kind of fruit.
All but five bowls contain some cherries,
all but four contain some apricots, and
all but three contain some red currants.
How many bowls were at the dinner?
 On average there are 100,000 strands of hair on a person's head.
On average there are 100,000 strands of hair on a person's head.
Hair grows at a rate of about 15cm a year and each hair lasts up to 6 years before it falls out.
If two sisters have 222,222 strands of hair together, and one has 20% more hair than the other, what is correct?
 Gerry won 30% of the first 40% of the annual Discus Throw competitions.
Gerry won 30% of the first 40% of the annual Discus Throw competitions.
What percent of his remaining competitions must he win to finish the year with 50% wins?
 Six students travel in a car.
Six students travel in a car.
How many different ways can they take seats if only 3 of them may drive and there are no empty seats?
 Three parrots yell at Gerry every 5, 7 and 9 seconds, respectively.
Three parrots yell at Gerry every 5, 7 and 9 seconds, respectively.
If they start yelling at Gerry at 6:00:00, how much time will elapse until they yell at Gerry at the same time again?
 I can cut off 4 circles from a circular sheet of dough.
I can cut off 4 circles from a circular sheet of dough.
I use the left-overs from 3 dough sheets to produce a new one.
How many circles can I make from 20 dough sheets?
 There are two gods named Orbis and Fidelis, one on your left, the other on your right, but you do not know which is which. Fidelis always answers correctly. Orbis only answers alternate questions correctly; you do not know if his last answer was correct.
There are two gods named Orbis and Fidelis, one on your left, the other on your right, but you do not know which is which. Fidelis always answers correctly. Orbis only answers alternate questions correctly; you do not know if his last answer was correct.
You must determine which god is which using the minimum number of YES/NO questions. How many questions do you need to be certain?
To clarify the matter, if Orbis is answering incorrectly your entire question is evaluated correctly and then the answer is reversed. A single question to both gods counts as two questions.
Author : Leslie Green
Inspired by G. Boolos. 'The hardest logic puzzle ever', The Harvard Review of Philosophy (6), 1996.
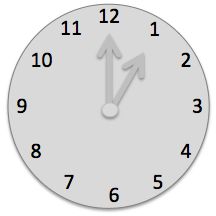 Divide the analog watch face with five straight parallel lines so that the sums of the numbers in each part are equal.
Divide the analog watch face with five straight parallel lines so that the sums of the numbers in each part are equal.
What is the sum?
 Leslie Green asks:
Leslie Green asks:
I am allergic to washing powder, but I don’t want my shirt to smell. The dermatologist has told me to reduce the total amount of washing powder residue on my shirt to less than 1 pico-gram. (I think he just made that number up on the spot!)
My dry shirt measures 280g, but after washing and spin-drying it weighs 350g. The washing and rinsing uses 21 L of fresh water for each operation. I wash my shirt with one 30g tablet of washing powder.
How many times do I have to rinse my shirt to reach the required non-allergenic state?
(remember that the density of water is 1g / mL, 1000 mL = 1 L, 1 pico-gram = 10-12g).
 Leslie Green tells a story and asks :
Leslie Green tells a story and asks :
It has been several years since the Apocalypse, but the Zombies still seem to be everywhere. I have been caught out in the open on my own and am now surrounded by 3 hungry Zombies, intent on eating my brains. Fortunately I have 6 rounds (“bullets”) in my gun. Unfortunately the ammo is old and degraded so it only works 80% of time. Also, although my aim is excellent on a shooting range, my shots are inaccurate when I am nervous, for example when I am surrounded by Zombies! It turns out that the closer they get, the more nervous I get, so the chance of my getting a shot to their head is only 63%. (Everybody knows that only a shot to the head will kill a Zombie). I worked it out, there is roughly 50% chance that any particular round will end up killing a Zombie.
There is just enough time to fire off all 6 rounds.
What is my chance of living to fight another day?
 Leslie Green asks
Leslie Green asks
A phrase you will hear on the news or from people speaking is "the vast majority of".
As a silly example you might hear something like
"The vast majority of people with big noses also have big ears."
What is the mathematical definition of the phrase "the vast majority of"?
 The chocolate biscuit factory you are now in charge of has a problem. There are three 8 hour shifts and 11 shift supervisors who each have their own treasured setup of the machines to give an optimum biscuit pass rate. Every time the controls are adjusted the pass rate drops for several hours until the process settles down again. Each supervisor adjusts the controls to their “optimum” settings when their shift starts! Having analysed what they are doing, you have summarized the settings into 11 controls with two positions each. You need to devise a series of experiments to establish the optimum settings in a convincing manner to improve the productivity of your plant.
The chocolate biscuit factory you are now in charge of has a problem. There are three 8 hour shifts and 11 shift supervisors who each have their own treasured setup of the machines to give an optimum biscuit pass rate. Every time the controls are adjusted the pass rate drops for several hours until the process settles down again. Each supervisor adjusts the controls to their “optimum” settings when their shift starts! Having analysed what they are doing, you have summarized the settings into 11 controls with two positions each. You need to devise a series of experiments to establish the optimum settings in a convincing manner to improve the productivity of your plant.
What is the minimum number of experiments necessary to find the optimum settings for each control?
Author: Leslie Green
 Leslie Green asks:
Leslie Green asks:
Peter changes his old fashioned single 100W incandescent light bulb to a super efficient 4 LED bulb system which gives the same light output, but only consumes 20W in total.
Estimate the saving per year if the bulbs are switched on for 8 hours every day of the year and you pay $0.1 per kWh.
(1 kWh is 1000 Watts for 1 hour)
 Forty-eight liters of water are poured into an aquarium of dimensions 50cm length, 30cm breadth, and 40cm height.
Forty-eight liters of water are poured into an aquarium of dimensions 50cm length, 30cm breadth, and 40cm height.
How high (in cm) will the water rise?
[1 liter = 1,000cm3]
This is a typical SAT question.
 You are pitching your new idea to a panel of Venture Capitalists (VCs) to secure increased funding. Using your advanced mathematical skills, you have dumbed-down the probability of success to something even VCs can understand. You tell them that if they were to throw 10 normal dice and sum the dots on top, the probability of your success is the same as the sum being less than 50.
You are pitching your new idea to a panel of Venture Capitalists (VCs) to secure increased funding. Using your advanced mathematical skills, you have dumbed-down the probability of success to something even VCs can understand. You tell them that if they were to throw 10 normal dice and sum the dots on top, the probability of your success is the same as the sum being less than 50.
One of the VCs seems very antagonistic, but you must still give the best possible answer, quickly – and using only mental arithmetic.
His question is "Can you guarantee that the sum of dots would be less than 50?"
Author: Leslie Green
 There are only two handshakes in a meeting: John shakes hands with a person, this person shakes hands with Anna.
There are only two handshakes in a meeting: John shakes hands with a person, this person shakes hands with Anna.
Does a man shake hands with a woman in the meeting?
 What is the main difference between the pictures on the left page and on the right page?
What is the main difference between the pictures on the left page and on the right page?
The problem is similar to 100 Bongard Problems on visual pattern recognition.
 These are two identical six‐sided dice. The opposite faces of a die add up to 7.
These are two identical six‐sided dice. The opposite faces of a die add up to 7.
What is the sum of the number of dots on the two faces that touch each other?
 The teacher walked into her classroom to find a scene of devastation. There was red paint on the walls, her lunch had been half eaten, and books were thrown around the room. There were only three children in the room: Alex, Betty, and Clive.
The teacher walked into her classroom to find a scene of devastation. There was red paint on the walls, her lunch had been half eaten, and books were thrown around the room. There were only three children in the room: Alex, Betty, and Clive.
All three said that Betty ate the lunch. Betty said Alex painted the wall.
Clive said that Alex threw the books. Alex said that Clive painted the walls.
The Headmaster was called in to resolve the crisis. On his way to the scene he found Wesley hiding in the corridor. Whilst Wesley would not directly implicate anyone, he did admit (under duress) that each of the three had done one of the crimes, and that every statement they made had been untrue.
Given that Wesley is telling the truth, who threw the books?
Author: Leslie Green
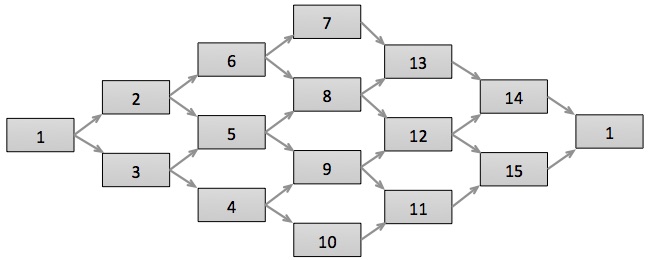 The picture shows a project plan. Arrows indicate where an activity must be finished before the next activity can start. The number shows the duration of the activity in days. An activity is critical if a delay by 1 day delays the whole project.
The picture shows a project plan. Arrows indicate where an activity must be finished before the next activity can start. The number shows the duration of the activity in days. An activity is critical if a delay by 1 day delays the whole project.
How many critical activities are there?
 The average score for dance of boys and girls in class A are 16 and 21, respectively.
The average score for dance of boys and girls in class A are 16 and 21, respectively.
The average score of boys and girls in class B are 15 and 20, respectively.
Twenty percent of class A students are girls.
Forty percent of class B students are girls.
Which class has a higher average score?
 A jeweler has 2016 pieces of chain, each with two links. He wants to make one big closed chain of them. To do this he has to open some links and close them afterwards.
A jeweler has 2016 pieces of chain, each with two links. He wants to make one big closed chain of them. To do this he has to open some links and close them afterwards.
What is the smallest number of links he has to open?
 Number SEVEN is mystic and frequently used in human culture.
Number SEVEN is mystic and frequently used in human culture.
What is the most reasonable cause of that fact?
 Four teams are in group A of a soccer (football) tournament for young girls.
Four teams are in group A of a soccer (football) tournament for young girls.
Each team plays one match against each of the other teams, with three points for a win, one point for a draw and none for a defeat.
If the three teams that pass to the next stage get 5, 4 and 4 points, how many points does the losing team get?
 Logic Puzzle.
Logic Puzzle.
Many years ago a king of a North European country decided to establish which is more dangerous for health: tea or coffee.
He ordered that one prisoner should only be given coffee, and that another prisoner should only be given tea.
What do you think? Who died first?
 Leslie Green asks:
Leslie Green asks:
Two hundred and thirty two boys and two hundred and twenty nine girls came out of school at different speeds.
After a while, 38 adults rushed out of the same building even faster than the kids.
The question: 'How many students and teachers went home after school?' has already been asked of 10 year olds, to which the correct answer was 499.
Now we ask a deeper question.
How many reasonable assumptions had to be made to get the correct answer?
 Gerry arranged the digits 2 through 9 in a particular order as follows:
Gerry arranged the digits 2 through 9 in a particular order as follows:
8 5 4 9 7 6 3 2
Where should the digit 1 be placed in this order?
 Leslie Green asks:
Leslie Green asks:
Here is a number sequence with a definite mathematical rule to move from one number to the next.
3, 7, 11, 17, 27, 43
The tricky thing is that one number (not necessarily at the end) has been deleted from the sequence, but which number?
(Hint: This is just mathematics. It works in any language, not just English.)
 Leslie Green asks:
Leslie Green asks:
In many homes, old and new, you find radiators directly underneath the windows.
Why?
 One hundred and one coins have the property that when one is removed, the others can be divided into two groups having equal value.
One hundred and one coins have the property that when one is removed, the others can be divided into two groups having equal value.
If three coins have 3-piastra value, what value do the other coins have?
Inspired by: The USSR Problem Book by Shklarsky, Chentov, and Yaglom, Freeman, 1962.
 When my coconuts were counted in twos, there was one extra.
When my coconuts were counted in twos, there was one extra.
When counted in threes, there were two extra.
When counted in fours, there were three extra.
When counted in fives, there were four extra.
When counted in sixes, there were five extra.
When the coconuts were counted in sevens, no extra coconut was left.
What is the minimum number of coconuts I could have?
 For every day in January, Gerry sent three letters, one to each of his three girlfriends.
For every day in January, Gerry sent three letters, one to each of his three girlfriends.
The postman put the letters into three different boxes without looking at the name of the recipient.
For ten of the days, nobody received their letters correctly.
For twelve of the days, only one girl received her letter correctly.
For how many days did all three girls receive their letter correctly?
 A printer sometimes moves certain characters up. It can print
A printer sometimes moves certain characters up. It can print
23 53
instead of
2353
The first can be interpreted as the product of
23 = 8 and 53 = 125 that is 2000.
These two numbers are different.
Is there a 4-digit number that does not change its value when two of its digits move up?
The solution was suggested by Henry Ernest Dudenay in the book Amusements In Mathematics, 1917