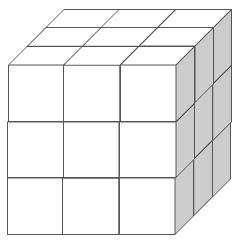
There are 9 squares on each side of a cube.
We paint each square either blue, yellow, or green.
Squares of the same colour must not have common edges.
What is the largest possible number of blue squares?
There are 9 squares on each side of a cube.
We paint each square either blue, yellow, or green.
Squares of the same colour must not have common edges.
What is the largest possible number of blue squares?
Delete a white stroke to make the equality correct.
In what symbol (including the numbers) of the equality do you delete it?
What is the number of different ways to paint the six faces of a cube with six different given colours?
Two ways are different if one cube cannot be rotated to look like the other.
The red small circles are midpoints of the corresponding sides of the 1x1 square.
Find the ratio of side lengths of the green triangle.
Type the number of seconds in a week using the smallest number of characters.
How many characters do you use?
How many straight line segments connecting two points can be placed without forming a triangle with three points as vertices?
Find the largest possible number.
Move just one matchstick to make the largest possible number.
From which number do you choose the matchstick?
Jane celebrates her birthday today.
She prepared a circular cake with the diameter of 20 cm and put as many candles as her age.
Her mom insisted that the distance between two candles is at least 4 cm and the distance from the outer perimeter of the cake to a candle is at least 2 cm.
She put as many candles as possible and it was exactly her age.
How old is Jane?
The picture show the cake surface, a candle in the center, and a circle of diameter 4 cm around the candle.
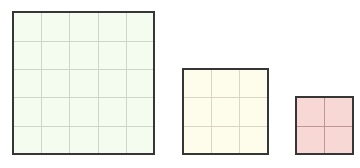Gerry places at least one 5x5 cm square tile, at least one 3x3 cm square tile, and at least one 2x2 cm square tile on a large wooden square. All the surface of the wooden square is covered by the tiles without gaps and without overlapping.
What is the smallest possible number of tiles on the wooden square?
Gerry cut a cube by three straight cuts parallel to the cube faces, painted the parts either green or yellow, and then put them back together again.
There are four yellow and four green cuboids.
Estimate which surface area is the greatest.
The first line shows that the product of three decimal fractions is another decimal fraction.
Replace the six asterisks in the second line by non-zero digits so that the product of the three decimal fractions is equal to 10. Some of the digits can be the same.
What is the sum of the six digits?
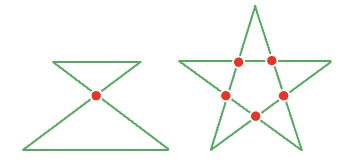We connect line segments end-to-end to make a loop with maximum points where two lines cross.
Four lines segments have one such a point.
Five line segments have five such points.
How many intersection points can we obtain with seven line segments?
Inspired by James Tanton's puzzle.
In a coffee shop, 13 individual tables are in a line. People take tables only if both neighbouring tables are unoccupied, otherwise they leave the shop. The shop owner wants as many customers as possible. She tells the first customer where to sit. All the other customers will pick the farthest possible table from other customers.
Which first table do you choose?
Inspired by a puzzle from puzzlesworld.com
On a dark night, two pirates try to divide a pile of golden ducats equally among them. When they divide the coins equally, a coin was left. They awaken the third pirate and divide all the coin equally again. A coin is left. The story repeats with four, five, and six pirates. Only seven pirates equally divide the coins.
What is the minimum possible number of ducats in the pile?
Earth's circumference (the distance all the way around the equator) is 24,901 miles (40,075 kilometres).
There are three airplanes on an airbase in Ecuador. Each plane has a fuel tank that holds just enough fuel to allow the plane to travel half the distance around the equator plus 7 miles. These airplanes are able to transfer fuel between their tanks in mid-flight.
Estimate the maximum distance a single airplane can theoretically travel around the word as a fraction of the Earth's circumference.
The chessboard was not correctly painted.
We need to cut it by straight cuts and reassemble together. The pieces don’t move until the last cut is made.
What is the least number of cuts needed to form a standard chessboard with alternating dark and light squares?
The chessboard was not correctly painted.
We need to cut it by straight cuts and reassemble together. The pieces don’t move until the last cut is made.
What is the least number of cuts needed to form a standard chessboard with alternating dark and light squares?
Job Interview Puzzle
You have a flash light which needs 2 good batteries to run, and 12 batteries, 6 good ones and 6 completely empty.
In the worst case situation, what is the least number of trials needed to get the flashlight running?
Note that even when we know which are the good batteries, we still count making the flashlight shine as a trial.
Three ants begin to crawl when the traffic light becomes green. They crawl only on the red part of the triangular sign. Each of them randomly chooses one of the two possible directions.
What is the probability that two ants don't collide?
This puzzle is called a word ladder.
We change one letter at a step, always spelling real words:
LEAD → LOAD → TOAD → TOLD → GOLD.
We manage to do it in 4 steps.
Using the same technique, turn HEAD into TAIL.
What is the least possible number of steps for that?
Four friends are collecting money for their summer trip.
They have already collected a certain amount of money S.
If Alex doubles his share, then the sum S increases by one sixth.
If Betty doubles her share, then the sum S increases by one fifth.
If Craig doubles his share, then the sum S increases by one fourth.
Who contributes more money?
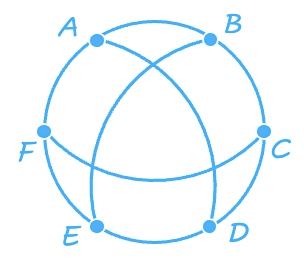There are 6 airports in a kingdom. Some of them are connected by direct flights. If two airports X and Y are connected by a direct flight, and airports Y and Z are also connected by another direct flight, then a direct flight between cities X and Z is considered to be decadent, and therefore not permitted.
The picture shows 9 direct flights between 6 airports.
The government decided to open 6 more airports.
What would be the largest possible number of direct flights in the kingdom after that?
An eight-sided polygon is an octagon.
What is the largest number of triangles that can be obtained from a paper octagon by a single straight cut?
On an island, every family has two children.
70% of girls have a sister.
40% of boys have a brother.
How many times more girls than boys are there on the island?
Eight figure skaters participate in a competition. Each of three judges independently assigns places 1 to 8 to the skaters, where 1 is the best. The skater with the smallest sum of the places was the winner.
All the judges gave the same place to the only winner.
What is the largest (worst) possible placing the winner could have received?
John and Mary share a delicious triangular cake, the sides of the triangle being equal. John chooses a point on the cake, and Mary makes a straight cut through that point, taking the larger piece. Both teenagers want to get as much as possible.
What part of the cake might John obtain if his girl-friend is very strong in geometry?
The red points are mid-points of the corresponding sides of the square.
Find the area of the blue quadrilateral if the area of the square is 400 cm2.
Girls and boys, totalling 33, hold hands in a circle.
Twenty of them hold hands with at least one boy.
Twenty seven of them hold hands with at least one girl.
How many girls are there?
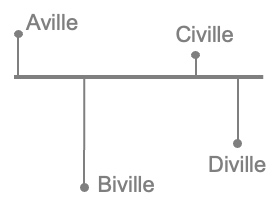An old postman remembers almost all the distances in his county:
Aville - Biville = 10 miles,
Biville - Civille = 11 miles,
Aville - Civille = 11 miles,
Biville - Diville = 15 miles.
He does not remember the distance between Aville to Diville.
Can you find it?
Alex, Bill and Carl have a collection of balls of three colours.
We know that there is
a green ball among any 5 balls of their collection,
a red ball among any 6 balls, and
a blue ball among any 7 balls.
How many green balls are there in their collection?
Ten girls participated in a competition. The participants are stable in their performance: the stronger fighter always wins against the weaker fighter.
Everybody fights twice, with no draws, and with no rematch with the same fighters.
Those who win twice get a prize.
What is the least possible number of prizes?
An architect is planning to build 25 cities on a square grid and connect them by straight roads. The roads can be either 10 miles long on the sides of the square grid or 7 miles along the diagonals.
What is the least possible total length of the roads so that people would be able to drive from one city to any of the others?
Two bikers travel on an island.
Today, one is in city A and the other in city H.
Every day they travel to a randomly chosen neighbouring city that is linked by a straight road.
In which city can they meet?
The Eiffel Tower is a wrought-iron lattice tower in Paris, France. It is named after the engineer Gustave Eiffel, whose company designed and built the tower. The main structural work was completed in 1889. The tower is 330 metres (1,083 ft) tall, about the same height as an 81-storey building, and the tallest structure in Paris.
At which of the four dates was the tower the tallest?
Ninty-six applicants take a tricky job interview test with 25 questions with one point for the correct answer.
Which score is nobody able to obtain?
What is the minimum number of weighing operations required to measure 15 kilograms (kg) of cacao beans if only a balance scale and one weight of 1 kg are available?
Alex, Bill, Carl, and David play a game. One by one (in the alphabetic order) they break the Swiss chocolate bar along the lines until all the pieces are 1x1 bars. Nobody cannot break two or more pieces at once.
The last person who is able to separate a bar is the winner.
Do you know a winning strategy? Who is the winner?
Gerry found an old book with the text
We bought 72 eggs for $_5.4_
The first and the last digits of the price were not legible (readable).
Can you find the exact price of the eggs?
The average annual income of a family is 240 thousand dollars in Richland and 100 thousand dollars in Poorland.
The move of 4 families from Richland to Poorland increases the average incomes in the two villages by 40 thousand dollars.
How many families live in the two villages?
Area maze puzzle (menseki meiro in Japanese)
The picture shows the areas and widths of the corresponding rectangles.
Find the area of the green rectangle.
Gerry's salary is 60% of his boss's salary.
By what percentage should his boss's salary decrease and Gerry's salary increase to become equal?
A goldsmith has 12 double-links of chain.
The craftsman wants to make a single closed chain out of the links.
What is the minimum number of links that he must open and close again?
A player threw 6 darts at a board three times. We don't know the values of the rings, but we know how many points he got the first two times.
How many points is the third game worth?
A shoe lace is lying on a table, with as many crossing points as shown in the image.
The lace is equally likely to pass over itself or under itself when we move from one end to another.
What is the probability that the shoe lace is knotted after its ends are pulled?
Avany and Bavany are twin sisters who walk with the same walking speed, and run with the same running speed.
They take a trip to their Granny's cottage.
Avany walks for half the distance, and runs for half the distance.
Bavany walks for half the time, and runs for half the time.
Who is the first to arrive at Granny's cottage?
Anna and Betty are running at constant speeds on a circular track.
If they run in opposite directions, they meet after 1 minute.
If they run in the same direction, they meet after 5 minutes.
How much faster is Anna running than Betty?
A cowboy gallops into a town on Friday, participates in a rodeo, stays for two days, and leaves the town on Friday.
How many days does he stay in the town?
The photograph courtesy of Roland Sauter
What is the largest number of matchsticks you can place on a table so that each matchstick touches all the others?
Job Interview puzzle
There are 77 knights in a circle. The first knight touches the second one and the second knight must leave the circle. Then the third does the same with the fourth and so on. The knight who is left alone in the circle receives the crown and becomes the king.
Which is the number of the last knight?
Job Interview puzzle
A clever merchant passes 5 checkpoints in a country. He has 5 bags with 5 delicious melons each. No bag can hold more than 5 melons. On each checkpoint he has to give one melon for each bag with melons.
How many melons are left after crossing all the checkpoints?
A sailor finds himself on an uninhabited island after a shipwreck. A couple of days later, 33 wild warriors visit the island. They decide that one of them will kill the sailor. They give him the right to choose the "killer". The sailor tells them his choice. The warriors leave the island without killing the sailor.
How does the sailor state his choice?
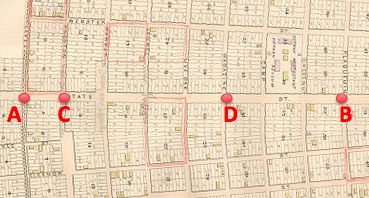Anny, Benny, Canny, and Danny want to meet somewhere on their street, so that the sum of the distances they walk is the smallest.
What is the best place to meet?
Three doctors have an elder brother, John who works as the mayor of their city.
John has a wife, two children, two parents, who all live in the same city, and no brothers.
How many children do John's parents have?
A job interview brainteaser.
What is the least number of matchsticks which have to be moved so that the 10 matchsticks form a picture with an axe of symmetry?
A side of a right triangle is 112 feet and its hypotenuse is 113 feet long.
What is the length of the third side of the right triangle?
You don't need a calculator to find the answer.
A job interview logic puzzle.
Add a line segment to the image so that we can interpret the writing as a time.
What is the time?
After riding 5 miles from his home towards Jane's house, Gerry discovered that he had lost his bag with a present for Jane.
He rode back and found it 20 minutes later.
After riding for another 10 miles, he arrived at Jane's house.
They spent a wonderful afternoon together and he rode back home.
What total distance did he ride that day?
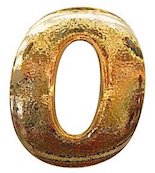0 0 0 0 0
Make a result that is greater than 100 using only 5 zeros and any mathematical symbols.
How many plus signs do you use?
Three pirates share 6 bags with 12, 18, 21, 21, 21, 25, and 27 golden ducats without opening the bags.
The first pirate takes some money.
The second pirate takes twice as much as the first pirate.
How much money does the third pirate take?
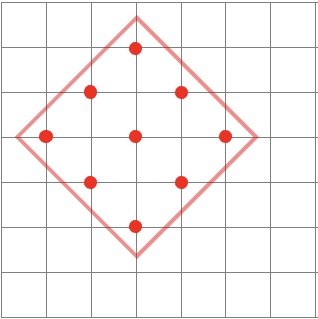
The nine red points form a triangle.
What is the least number of the points that have to be moved to form a square?
The nine red points form a square.
What is the least number of the points that have to be moved to form a triangle?
Draw the outline of a shape inside the square so that it separates the square area into five shapes, four of which are the same.
What is the new shape?
What number is missing?
Find the odd one out.
What number is missing?
Twins John and Jane left a building without having ever entered it.
What was the building?
21x + 3y = 233
How many integer solutions does the equation have?
Estimate the diameter of the green circle if the diameter of the yellow circles is 1.
Choose a positive integer that is smaller than one hundred, add 7, multiply by 3, subtract 1, and divide by the number that you get.
What is the result?
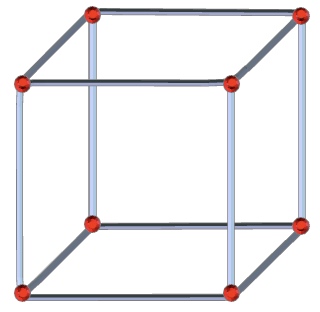A plumber bends wire and welds a frame of a cube.
What is the least number of separate pieces of wire needed to assemble the cubical frame without repeating an edge?
1 + 2 + 3 + ... + 2022
What is the result?
The length of hypotenuse of a right triangle is 10 cm.
What is the largest possible area of the triangle?
A hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle (90°).
Jane has two rectangular sheets of paper of the same sizes.
She puts the green sheet on the blue sheet so that the two green corners are on the blue edges and one of the blue corners is covered.
What area of the blue sheet is greater?
How many 9s are there in the result of the multiplication:
1111 x 9999 ?
Don't use a calculator.
John must play three singles matches against his parents.
If he wins two matches in a row he gets money for a new computer.
His father is a better player than his mother.
Should he play Mother-Father-Mother (M-F-M) or some other order?
There are 15 desks arranged in 5 rows and 3 columns in a classroom. The teacher asks each student to move to the desk in front of, behind, to the left of, or to the right of the current desk.
With a suitable strategy, is it possible for every student to be able to move to a new seat?
Two friends decided to meet near a river.
At what point on the river bank should they meet in order to minimize the combined lengths of their trips?
Noboyuki Yoshigahara noticed this sign on the glass door of an Osaka restaurant.
What does it mean?
There are four balls in a bag.
A magician draws two balls, one of them is white.
What is the probability that the other is white?
A seller has a bag of gold dust, an unbalanced scale, and 1-ounce weight.
What amount of gold dust can he weigh?
1 troy ounce ≈ 31.1 grams
Which point on the line has the smallest sum of distances to the labelled points?
In a bullring, a torero runs from a bull with a constant speed of 10 meters per second.
He starts at a point on the ring's edge, and runs straight for 4 seconds, at which time he reaches the ring's edge again. He turns right by 90° (relative to his earlier straight path) and runs straight for 3 seconds, at which time he not only reaches the ring's edge, but also finds the escape exit.
Fortunately, he is still alive.
What is the ring's diameter?
A mother and her daughter start walking together with the right foot.
The mother takes two strides to her daughter’s three.
When will they first step together with the left foot?
The problem was found in Futility Closet collection.
Four 1-inch sticks form a small square.
Four 2-inch sticks form a large square.
Can you rearrange the 8 sticks together to form more than 2 smaller squares of the same size?
A stick can cross another stick. Spare parts outside the squares are not allowed.
Inspired by a Sam Loyd's puzzle.
A young couple would like to have four children.
Which of the following is more likely?
The country's statistics shows that each birth has an equal chance of being a boy or a girl.
Find x.
I turn up the cards in pairs from a shuffled deck. Two red cards are yours. Two black cards are mine. If one is black and one red, then they belong to no one.
You pay only a dollar for the privilege of playing the game. When the game is over, for every card that you have more than I, I will pay you N dollars.
- From Edward Barbeau, Murray Klamkin, and William Moser, Five Hundred Mathematical Challenges, 1995.
What is the least prize, N, that is profitable for you to play?
Starting in one of the states that are marked by light green on the map, you must travel through the 48 contiguous United States, visiting each state exactly once.
Which colour on the map is the last state of your trip?
Inspired by Futilitycloset End State Problem.
The sum of the five coloured angles is . . .
The numbers show the areas of the corresponding parts of the square.
Find the area of the red region.
Find the two heaviest stones among 16 stones, all of different weights, by using an equal-arm balance.
What is the least number of weighings needed?
The Rhind Mathematical Papyrus (1550 BC) is one of the best known examples of ancient Egyptian mathematics.
One of its problems was to calculate how many pebbles fit inside a circle having a diameter of 9 pebbles.
Can you make the estimation using modern knowledge of geometry?
Move one stick to make the equality true.
From which part do you move the stick?
A safe is protected by a three-digit binary (0 or 1) combination.
The safe only considers the last three digits entered when deciding whether an input matches the passcode.
23 = 8 passcodes are possible.
We have to input 3 x 8 = 24 digits in the worst case.
Can we stream a smaller number of digits?
What is the shortest stream of digits that includes all 8 passcodes?
"You take a spoon of wine from a barrel of wine, and you put it into your cup of tea. Then you return a spoon of the (nonuniform!) mixture of tea from your cup to the barrel. Now you have some foreign substance (wine) in the cup and some foreign substance (tea) in the barrel.
Which is larger: the quantity of wine in the cup or the quantity of tea in the barrel at the end of your manipulations?"
by Vladimir Arnold.
There are 25 horses. We can take 5 horses at a time and race them. Each horse always finishes the race in the same amount of time, and there are no ties. The only information you get from each race is the order that the 5 horses finished in.
What is the smallest number of races that are needed to find the 3 fastest horses?
Gerry places 78 cherries in a line.
First day he eats every seventh cherry in the line.
Next day he eats every sixth cherry in the line.
Next day he eats every fifth cherry in the line.
Next day he eats every fourth cherry in the line.
Next day he eats every third cherry in the line.
Next day he eats every second cherry in the line.
Next day he eats all the cherries that are left.
On which day does Gerry eat more cherries?
There is a species of animal capable of jumping higher than the average house.
Which is it?
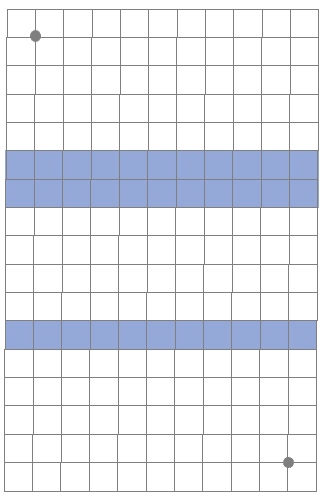Chief Road Officer of Wonderland (CROW), Crock Cross, plans to build a road between 2 cities that perpendicularly crosses two rivers.
The cities and rivers are shown on a 1-km grid.
Estimate the length of the shortest road between the two cities.
We form a 5x5 grid from 36 small wooden sticks.
There are many different squares in the grid: 1x1, 2x2, 3x3, 4x4, and 5x5.
What is the least number of sticks to remove, so that there are no 2x2 squares?
Jane puts 15 playing cards on a table, face down. Gerry is blindfolded so he cannot see the flip-states of the cards, but he can feel where they are. Jane arbitrarily flips 5 cards face up.
Gerry separates the cards into two unequally sized groups of his choosing, and optionally flips any number of cards whilst still blindfolded. If Gerry manages to have the same number of face-up cards in both groups he wins.
Gerry wins this same game repeatedly, suggesting that his method is not random chance.
What is the number of cards in the smallest group?
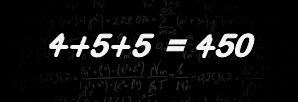Add a stroke to make the equality correct.
In what symbol (including the numbers) of the equality do you draw it?
There are 19 stones in the third ring, 26 stones in the fourth ring, 33 stones in the fifth ring, and 39 stones in the sixth ring.
Estimate the number of stones in the tenth ring.
Zeno of Elea (495 – 430 BC) was a Greek philosopher. He is best known for his paradoxes.
One of his paradoxes suggests walking half of the distance that is left instead of walking all the distance from one place to another. Zeno of Elea transformed a short distance into an infinitely long list of halved remaining distances, all of which are greater than zero. And that was the problem: how can a distance be short when measured directly and also infinite when summed over its infinite list of halved remainders?
Now we consider a practical problem. If the distance between two places is one thousand steps and a girl walks half of the remaining distance every hour, how much time does it take to arrive at a distance to the destination that is smaller than one step?
A cross is formed by 5 squares.
Cut the cross along straight lines and rearrange the pieces of the cross into a square.
No overlapping of, or gap between, the separate pieces is allowed.
What is the least number of cuts?
Surprise your friends with a trick!
Roll two standard dice and ask them to calculate
(1) the product of the two top numbers
(2) the product of the two bottom numbers
(3) the product of the top number of the red die and the bottom number of the green die
(4) the product of the bottom number of the red die and the top number of the green die
If they add the four products, they always get the same result!
Which one?
Divide the interior space of the regular polygon with 2021 sides by non-intersecting diagonals into triangles.
How many of them are acute triangles?
All angles of an acute triangle are acute (less than 90°).
Amyra possesses 60% of a business and the rest belongs to Betty.
They take Chase into partnership so that the three partners have an equal interest in the business.
Chase pays 100 thousand dollars.
How much more money does Amyra receive than Betty?
A Swiss train completely passes by a tree in 1 minute, through a tunnel in 3 minutes and through another tunnel in 5 minutes. It travels at the same speed.
How many times is the second tunnel longer than the first one?
Three friends played chess games with each other all day.
Jim played 7 games and Jeff played 4 games.
What could be the number of games that John played?
Jane and Gerry take turns putting a 10-centime coin on a rectangular table so that the coins do not overlap each other.
Whoever cannot make a move loses.
Jane starts first.
Who wins if one of them knows the winning strategy?
To which part of the Americas do the following belong:
Antigua and Barbuda,
Bahamas,
Cuba, and
Dominica?
Which tire does not move when the car turns left?
Charlie belongs to London's top society.
During which month does Charlie sleep the least?
When you put the five puzzle pieces together correctly, they form a rectangle with a calculation on it.
What is the result of the calculation?
Arrange the digits 1, 2, 3, 4, 5, 6 to form two 3-digit integers whose difference is as small as possible.
What is the difference?
Five line segments coincide at a point.
What is the sum of the five marked angles?
A shopkeeper has equal stock values (in dollars) of each of two kinds of peas, which ordinarily sell for $2 per kilogram and $3 per kilogram respectively.
Unfortunately her idiot trainee has thoroughly mixed up all the peas.
What is the price she must set for the mixed peas, so that she sells them for the same amount of money as the separated peas?
Birth data for England and Wales has been used to look at trends in the most popular birth date over the past two decades.
Try to guess the month with the highest birth rate.
How many different triangles can you compose from the five line segments of lengths 1, 2, 3, 4, and 5 feet?
All the side lengths in any particular triangle have to be different.
The line segments can be used multiple times from one triangle to the next.
How do you measure a half-meter from a rope that is ⅔ meters long without any measuring tools?
An apple is floating in water so that ¼ of the apple is above water and ¾ is under water. A fish starts eating the apple under water at a rate of 20 grams per minute, while a bird starts eating the apple above water at a rate that is twice as big as the rate of the fish.
Which part of the apple will the fish eat?
There are 12 people in a line to a shop.
If Jane is the fourth from the beginning and Gerry is the third from the end, how many people are there between them?
Children who are standing in a circle do a headcount. Abby says one, her neighbour says two and so on. If they count in a clockwise direction, Michael says 15. If they count in an anticlockwise direction, he also says 15.
How many children are forming the circle?
Thirty-three European teams enter a tournament.
Each team plays one match against each of the other teams with three points for a win, one point for a draw, and none for a defeat.
If a team has 77 points at the end, what is maximum possible number of matches the team could have lost?
We remove green points until no three points lie on one line in the remaining diagram.
What is the maximum number of points that can be left in the remaining diagram?
Put the five puzzle pieces together.
What is the largest possible result of the calculation?
Five points are marked on a grid.
The side length of a small square is 1 cm.
Form a triangle using three of the five points.
What is the smallest area of the triangle that you can obtain?
The picture shows a map of the downtown of Los Math.
The length of a side of a city block is 20 metres.
How long is the path around the downtown?
Four identical blocks are glued together.
We need exactly one gallon of paint for all sides of a box.
How many gallons of paint are needed to paint the outside of the glued construction?
A seller chooses his meter rulers that are 2 cm longer for ladies and 4 cm shorter for gentlemen. This means for every meter (100 cm) of cloth a lady buys, she actually gets 102 cm of it.
By how much is Mary's piece of cloth longer than John's piece, if they both buy 4½ meters of cloth?
We think that he was born in 287 and died in 212.
Who is he?
The ages of a grandfather and his grandson add up to 99.
The grandson's age is the grandfather's age reversed.
How old is the grandfather?
Tom's mother has three children: Tic, Tac, and ….
What is the easiest way to make the following equation correct?
Connect 13 airports by airlines so that you can fly from any airport to any other one, making at most one change.
What is the least number of airlines that are needed?
A school bus is considered as "overloaded" if there are more than 50 students in the bus.
One hundred school buses, some of them overloaded, arrive at a school today.
What is greater?
A girl is waiting for a train at the train stop, freezing. She wants to walk to the next stop. She walks four times slower than the train and can see it at a distance of 1000 meters. It is exactly 500 meters to the next stop.
Does it make sense to walk, or is the risk of missing the train huge?
Twelve teams enter a hockey tournament.
Each team plays one match against each of the other teams with three points for a win, one point for a draw, and none for a defeat.
What is the largest possible difference of points of two neighbouring teams in the final table?
Two beautiful princesses, a certain distance apart, start walking at the same instant from the two initial points of a long straight alley with the same speed. They walk away from each other.
A prince is between them, but closer to the left princess. He wants to see the faces of both beauties as soon as possible to make an important decision. He walks twice as fast as the princesses in one direction and after meeting the first princess he changes to the opposite direction.
Which direction do you advise to choose first?
Find the most subtle error with the image.
Is there a point outside each of these two circles for which any line passing through intersects at least one of the circles?
If YES, where is it?
A guard in the middle of an empty room cannot completely see any of its walls, even if he turns around on that same spot.
What is the least possible number of walls in the strange room?
A 3-digit passcode uses 3 different digits: 7, 8, and 9.
The lock is opened if the digits are given in the correct order.
What is the least number of digits you need to press to be sure that the lock opens?
Jane's grandfather and grandmother left some dollar bills in an envelope for her to buy a present for Christmas.
Estimate how much more money her grandfather left than her grandmother.
Jane's grandfather and grandmother left some dollar bills in an envelope for her to buy a present for Christmas. Jane expected to buy a robe that is worth more than $160. Unfortunately there was a smaller amount of money in the envelope.
How much money could be in the envelope?
Separate all red points from green points by straight lines.
What is the least number of lines that are needed?
Take 16 coins and put them in four rows of 4 each. Remove 6, leaving an even number of coins in each row and each column.
What is the smallest number of coins in a row or a column?
Puzzle 21 from the book of Boris Kordemsky The Moscow Puzzles
The chair with long legs stays perfectly still (is not 'wobbly') on a horizontal surface. A carpenter cuts off small pieces of wood from all the four legs. The heights of three pieces were 30 cm, 40 cm, and 50 cm.
The chair with the new legs also stays perfectly still on a horizontal surface.
What can be the height of the fourth piece of wood?
What is the maximum possible number of triangles I can obtain by a single straight cut through the hexagon?
The boxing ring is 7 meters in length on each side between the ropes. An electrician installs 4 lamps which light a circle of the same diameter as the height of the lamp over the boxing ring.
Estimate the minimum possible height of the lamps that guarantees light over all the ring.
The original Olympic motto is made up of three Latin words:
Citius - Altius - Fortius
Guess what the words mean in English.
The English translation of the words is given below together with an additional non-related word.
Which word does not belong to the Olympic motto?
In Happy Land, people are happy, even though the prices grow by 40% in a day.
Gerry bought an apple and a pear today with the same money as two apples and a pear yesterday.
How much does a pear cost?
A granny makes the same amount of soup every day. Yesterday she made some soup without enough salt initially, so she had to add some salt at the end. Today she added a quarter more salt than she initially used yesterday, but she still had to add more salt at the end. Today, the added salt at the end was half as much as that added at the end yesterday.
Tomorrow, how much more salt should she use, compared to today's initial amount, so that she won't need to add more salt at the end?
Four pirates, Alvilda, Blackbeard, Calico, and Diabolito, share a treasure.
Blackbeard takes half of what Alvida takes.
Calico takes half of what Alvilda does not take.
Diabolito takes half of what Blackbeard and Calico take together.
Who takes more?
In a class, each girl has exactly 4 friends among the boys of the class and each boy has exactly 3 friends among the girls of the class.
How many students are there in the class?
Two pirates share 77 coins, and they both know exactly how many coins are being shared.
Johnny has the first pick, and decides on the number of coins to take. For each of his turns he can choose a different number of coins. The number of coins has to be at least 1, but not more than 10.
Luidgi always takes one coin more than Johnny took, provided there are still coins available to take. They take turns grabbing their piles of coins until the chest is empty.
How many more coins can Johnny take than Luidgi?
There are 33 humps in a herd of horses, one-humped camels, and two-humped camels.
The number of horses and two-humped camels is the same.
How many animals are there in the herd?
Inspired by a problem of the Moscow Mathematical Regatta, 2010
Mrs Shy said to her 24 students
"You are too young to see this. Please close your eyes."
All the boys and ¾ of the girls close their left eyes.
All the girls and ¾ of the boys close their right eyes.
How many student see 'this'?
A prime number is a positive integer that has no positive divisors other than 1 and itself.
2, 3, 5, 7, 11, 13, 17, . . . are prime numbers.
An isosceles triangle has two equal sides.
The three angle measures of an isosceles triangle in degrees are prime numbers.
What is one of the angles?
Inspired by a problem of the Moscow Mathematical Regatta, 2003 / 2004
I fold four square pieces of paper in half twice without unfolding, making 4 new squares. I cut them with a straight cut across the front face, and through all parts, and create a number of pieces.
What is the the total number of pieces that I obtain?
A grandmother has two grandchildren, Alice and Brice. Alice calls her every second day and Brice calls her every third.
What is the fraction of days when she does not receive a call from the lovely grandchildren?
A banker forgets which of the five correct keys fits in which of the five keyholes.
What is the minimum number of trials to identify which key is meant for each lock if you are not lucky?
Suppose the year is 2021 and somebody you know was born in 1950.
What is their maximum possible age?
NOTE: Leap years need not be considered.
Which number is the next in the sequence?
100, 99, 97, 94, 90, 85, ?
How many coins do you move to transform the rhomb into a triangle?
Find the smallest possible number.
Fifteen of 52 cards are face up in the deck. You are blindfolded and asked to divide the desk into two piles with the same number of face-up cards.
What is the number of cards in a pile?
The weed doubles the covered area in a pond every week. A farmer saw a 1-square-meter spot of weed 10 weeks ago and now the entire pond becomes covered by the weed.
On another pond of the same size, he sees two 1-square meter spots today.
How long does it take to cover the entire surface of the second pond by the weed?
John has decided to prepare himself a snack of a hot hard-boiled egg. He boils the egg in water for 7 minutes, then puts the egg into cold water in a dish to cool the shell before cracking the shell on the side of the sink. The shell is then easily removed. The egg is finally placed on a plate ready to eat.
What happens to the temperature of the outside of the egg?
Jane’s granny prepared a large basket of five different fruits for her granddaughter.
In the basket,
20 pieces are not apples,
22 pieces are not bananas,
24 pieces are not clementines,
26 pieces are not dates,
28 pieces are not egg-fruits.
How many pieces of fruits were there in the basket?
My parrot is being a real nuisance. Here am I, trying to not look like a pirate, and there he is going "Pieces of eight. Pieces of eight". In case you didn't know, a piece of eight is another name for a valuable Spanish silver dollar. I have 39 pieces of eight to split with my crew, who are definitely not pirates either. Half goes to me and half to the crew. In this case the crew is the first mate and an ordinary pirate, I mean "sea-man", because he is definitely not a pirate. The first mate gets five times more than the ordinary pir-, sea-man.
39 pieces of eight doesn't conveniently split as required, but I can make the split by giving away some of my ill-gotten-gains to the Sisters Of Mercy, thereby enhancing my cover.
What is the least amount I have to (reluctantly) give away?
Amongst us three siblings, I earn twice as much as my younger sister, Jane. Jane earns three times as much as her younger brother, John.
John claims to earn five times less than his older brother.
What sex am I?
In a knockout singles tennis tournament there were 13 matches.
How many sportsmen participated in the competition?
How many 3x4 mats are needed to cover the floor in a 34x34 room without gaps and overlapping?
The world population at 2021 was approximately 8 billion (8 thousand million).
Assuming that people use three names (first, middle, and family), that everyone requires a unique name, and that there is an equal number of each type of name, how many first names are required?
Gerry places 77 cherries in a line.
First day he eats every seventh cherry in the line.
Next day he eats every sixth cherry in the line.
Next day he eats every fifth cherry in the line.
Next day he eats every fourth cherry in the line.
Next day he eats every third cherry in the line.
Next day he eats every second cherry in the line.
Which day does Gerry eat more cherries?
How many L-shapes can be placed inside the circle without overlapping?
Find the maximum number.
Austin and Bart organize a duel.
They will take turns shooting at one another until one has been hit. We know that
1) Austin can hit Bart only 25% of the time,
2) Austin starts first, and
3) they have equal chances to be shot at the end of the duel.
What is Bart's probability of hitting his enemy in a single shot?
Logic question:
What is the largest of the four options?
Katie and Harry studied in a Summer Wizard School. They had the same skills at the beginning and the knowledge increased proportionally to the day of month, for example, it increases by 1% on September 1st, and by 13% on September 13th. He studied from September 1st to September 29th, while she from September 2nd to September 30th.
Estimate how much more skilful she got.
Which word is different compared to the three other words?
When you are promising to keep a secret, you often say,
"My lips are . . ."
The word "brunch" is formed from the combination of two words.
Which ones?
Which of these words is a common slang for an error in a computer program?
How many X's are there on a regular clock face with Roman numerals?
A proverb says
"A bird in the hand is worth two in the . . . ."
How does proverb end?
What is the last digit of the product of the first 77 positive odd numbers?
1 x 3 x 5 x 7 x 9 x 11 x 13 x 15 x 17 x . . . x 151 x 153
What is the expected number of times a fair die must be thrown until I get 3?
Two minutes ago, a boy said:
"One, two, three, Four and five,
I caught a hare alive;
Six, seven, eight, Nine and ten,
I let him go again."
How many hares does the boy have now?
Thomas Alva Edison was an American inventor and businessman who has been described as America's greatest inventor.
Which phrase belongs to Thomas Edison?
Mark Twain was an American writer, humorist, and entrepreneur.
Three phrases below belong to Mark Twain and one phrase to another person.
Which phrase does not belong to Mark Twain?
Albert Einstein was a German-born theoretical physicist who developed the theory of relativity, one of the two pillars of modern physics. He received the1921 Nobel Prize in Physics.
Which phrase belongs to Albert Einstein?
Mark Twain was an American writer, humorist, and entrepreneur.
Which phrase belongs to Mark Twain?
Walt Disney was an American entrepreneur, animator, film producer and a pioneer of the American animation industry. He introduced several developments in the production of cartoons.
Which phrase belongs to Walt Disney?
Which would eat more food in a day, a 70-kg man or a swarm of locusts that weighs 70 kg?
Alice bought a 100-gram chocolate square, having the same thickness throughout.
Unfortunately she dropped it, and it broke into 4 pieces as the picture shows.
It was broken by two perpendicular straight lines.
She weighed each piece.
Compare the lengths of the four sides a, b, c, and d.
You are buying a roller online on Amazon. Four similar rollers have the same functions, the same price, the same look, but different ratings.
Which product do you choose?
The diameter of the four watering cans (watering pots) is the same.
Which watering can is able to contain more water?
How much is a dozen halves of apples?
Correctly finish the rhyme.
Correctly finish the rhyme.
Correctly finish the rhyme.
Correctly finish the rhyme.
Correctly finish the rhyme.
What has more value?
How long is a rope that is two meters shorter than another rope that is two times the length of the first rope?
How many diagonals does the hexagon have?
The Head of Science in the small European country of Swedistan has decided to lead the world by converting to Metric Angles. In the new system there are 100.00° in a full circle.
What is the new rule for the sum of the internal Metric angles in a triangle?
Which wire is longer?
Which Russian doll is half the height of the tallest doll?
What is on the fourth card from the right?
At what age is a child half the height that he or she will be as an adult?
What is the least number of states that you must visit to bike from Austin, Texas to Los Angeles, California?
Which letter can you write without lifting the pen or retracing part of the letter?
A thumb war tournament had ten players: five girls and five boys. They form five teams of two players.
If the players are assigned so that all possible arrangements are equally likely, which of the following arrangements is more likely?
Estimate the number of people around the circle.
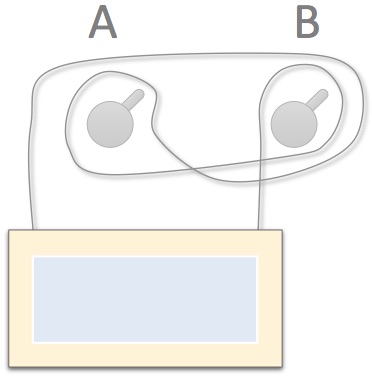I hung a picture frame on two nails as the scheme shows.
If I remove a nail does the frame fall?
Gerry has at least one dog, at least one cat, and at least one tortoise, as pets.
He has no other pets.
All of them are dogs, except for three.
All of them are cats, except for four.
All of them are tortoises, except for five.
How many dogs does he have?
Gerry wants to plant 7 trees so that there are as many rows of 3 trees as possible.
What is the largest possible number of such rows?
Is zero odd or even?
What is missing in the picture?
Gerry looks at the word in the rear-view mirror of his dad's car.
How many of the 11 letters look the same as the original?
My first is in bread and butter.
My second is in home, but not in hearth.
My third is in nut, but not bolt.
Which am I?
The relationship between a reed and a deer is similar, in some respects, to the relationship between evil and ...
My first is in chase, but not in chose.
My second is an a rush, but not in a bush.
My third is not in the cat, but is on the mat.
If you need a hand, I will give it to you.
What am I?
At what time do the clock hands form a straight line?
A security system relies on laser beams to detect intruders. When an object crosses a beam, an alarm rings.
What is the minimum number of the laser beams that must be installed to protect the access to a precious object and any of the laser sources.
The problem is planar (two-dimensional).
Chinese numbers are presented in the table.
Which is the largest number below?
In Square Island, each of its eight counties has a common borders with 4 neighbor counties.
How many counties have an access to the ocean?
Which word is coded below?
112119111
There are 13 pirates on a ship.
One pirate always tells the truth.
At least one pirate in any pair lies.
How many pirates are there on the ship who tell truth?
If you say its name, it disappears.
What is its first letter?
The Ninth Symphony of Beethoven is twice as long as the First Symphony.
If 12 musicians play the First Symphony in 30 minutes, how much time does it take for 6 musicians to play the Ninth Symphony of Beethoven?
A palindrome is a word, number, phrase, or other sequence of characters which reads the same backward as forward, such as racecar.
Punctuation, capitalization, and spaces are usually ignored.
Which phrase is not a palindrome?
There were about 200 countries (196 countries in 2010) in the world.
The country names start with almost all letters of the English alphabet, except
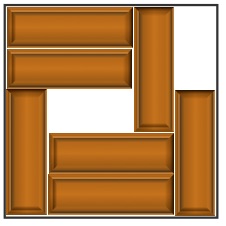Identical chocolate bars were arranged in a square box.
What is the least number of the bars that you need to slide in order to make room for one more bar?
It's me, and I will start at B.
Next is D, and next is G,
and then we have a K and P.
What's next?
If G is the first letter, and E is the third, which is the fifth letter?
John and his father are visiting a bar in Texas, USA.
If his father is 39 years old, how old is John?
Find the odd one out.
What does the picture show?
When is it safe to jump out of an airplane without a parachute?
Gerry uses L-shaped tiles to cover the 5 x 8 rectangle.
Certain tiles are not like the majority of the tiles.
How many tiles are odd?
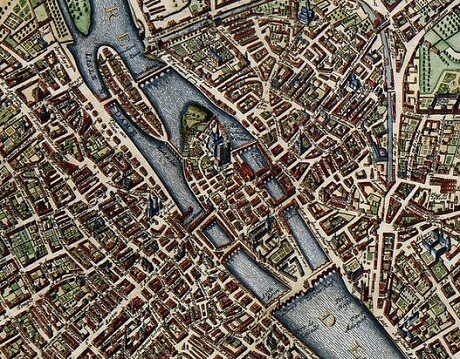In Paris, in 1657, of which the image shows a map, how many different ways were there to cross the river Seine using the bridges?
Please find the last number.
3 → 0
4 → 2
5 → 5
6 → 9
7 → ?
Hint : the MENSA question is linked to geometry.
About 37 million people live in the urban area of Tokyo, Japan.
Estimate how many boys there celebrate their birthday on April, 1st.
If ⅔ of SMALL is equal to ¼ of BIG, how many times is BIG greater than SMALL?
How old was Jane yesterday?
A dragonfly bears two pairs of wings and three pairs of legs.
Wikipedia says that dragonflies can travel at 100 body-lengths per second in forward flight, and three lengths per second backwards.
How many times does a dragonfly fly faster forward than backwards?
A group of 8 people go to a fishing trip.
There are 2 boys among them.
What is the maximum possible number of people who have sons in the group?
Alice is a well-educated, law-abiding girl. She goes to her school.
Can you guess the country where she lives?
A question at a job interview.
A bathtub is ¾ full of water.
You have a teaspoon, a teacup, and a bucket.
What would you use to empty the bathtub?
A helicopter starts from an Australian military base and flies 200 km south, then 200 km east, then 200 km north, and then 200 km west.
Where is it now compared to the departure point?
Which Roman number of the following has the smallest number of characters?
Do coconuts sink or float?
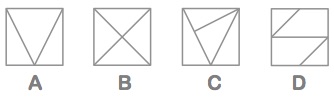Which diagram cannot be drawn without lifting your pencil off the page and without drawing along the same line twice?
A barber wants to write the word COOL on a board behind the client’s seat in such a way that a client looking in the mirror reads the word correctly.
Which of the following should the barber write on the board?
The first four Volumes of the Delicious Food Encyclopedia are stacked vertically side by side on a shelf. There 400 pages in each Volume.
A well-educated worm ate paper in a hole from the first page of the First Volume to the last page of the Fourth Volume.
How many pages did she taste?
There are 3 hockey pucks on ice.
A player shoots one of them between the two others. Then he repeats the shots always choosing another puck. He shoots all three pucks.
After how many shots can he get back to the original positions of the three pucks?
This is a standard set of dominoes.
I put all of them in a chain, for example 3 spots on one domino is connected to 3 spots on the next one.
If I have 2 spots on left end of the chain, what is the number of spots on the right end?
Jane wants to go from X to Y using the best shortcut.
Which points should she cross on the way?
A helicopter starts from a Canadian military base and flies 200 km south, then 200 km east, then 200 km north, and then 200 km west.
Where is it now compared to the departure point?
A large equilateral triangle is divided into 36 small identical triangles.
How many of the small triangles must be painted so that every small triangle touches at least one vertex of a painted triangle?
What is the ratio of the blue and green surface areas.
Which ring do you cut so that all rings are separated?
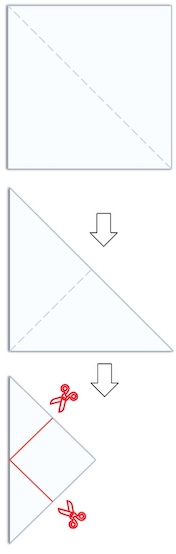Jane folded a square sheet of paper in half twice and then cut it twice, as shown in the diagram, before unfolding it all.
How many pieces does she obtain?
There is only one entrance into an apartment building via the ground floor.
One person lives on the first floor, two people live on the second floor, three on the third floor, four on the fourth floor, five on the fifth floor, six on the sixth floor, and one lives on the seventh floor.
Which button is more frequently used in the lift (elevator) of the building?
On Christmas Eve, Martin lit all seven small candles under the Christmas tree. He was so tired, that he immediately went to bed. His son Mark blew out three of them and also went to bed.
How many candles are left in the next morning?
Which 3 do you move to make the phrase correct?
The train moves to the east.
Which point of the wheels moves in the opposite direction?
I have 1 yellow, 2 green, 3 red, and 4 blue cubes.
I built a tower so that no cubes of the same color touch each other.
Which color is the cube in the middle?
I am nothing, not something.
You can see me only where I am not.
I am made from two things, yet I am still nothing.
What am I?
There is a mistake in one of the letters.
Which one?
In a preliminary stage of a competition a judoka fights with all others once. There is always a winner.
If 80% of the judokas won at least a match, how many contestants were there?
I fold a square piece of paper twice and cut it along the straight red line.
When it is unfolded, there is an equilateral triangle in the middle of the piece of paper.
If I need to obtain a square by a single straight cut in the same way, how many times do I need to fold a square piece of paper?
Which matchstick do you move to make the expression true?
Which matchstick do you move to make the expression true?
A runway numbered 09 points east (90°), runway 18 is south (180°), runway 27 points west (270°) and runway 36 points to the north (360° rather than 0°). There are two numbers at different ends of a runway. There is 13 at an end of a runway.
What is the number at the other end?
Which robot face belongs in the missing position?
by Leslie Green
I cut a square by 2 vertical and 2 horizontal straight cuts into 9 rectangles and write down their perimeters in the table.
One of the 9 numbers is not correct.
Which one?
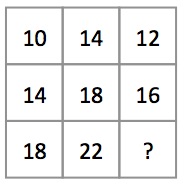Find the missing number.
I have a 'Christmas tree' that is green from both sides.
I would like to cut it into separate pieces and compose a rectangle.
What is the minimum possible number of straight cuts I should make?
Which symbol belongs in the missing square?
Which letter comes next in the sequence?
Which letter comes next in the sequence?
Which number should replace the question mark?
A banker has a brother, who is a plumber. The plumber is married to a nurse and they have two children - two boys.
Which statement can be true?
A spoke is one of some number of rods radiating from the center of a wheel (the hub where the axle connects), connecting the hub with the round traction surface.
If a wheel has 14 spokes, how many spaces between the spokes are there?
How many mistakes are there on the blackboard?
Gerry had 12 apples.
He ate several apples, less than half.
Then, he ate all but four.
Then, he ate half of them.
How many apples are left.
I once saw a line of elves. There were three elves behind an elf, three elves in front of an elf, and two elves in the middle.
What is the smallest number of elves there could have been?
You have four pieces of different colors. The cubes of the same color are glued together.
What top view is possible if you put these four pieces together?
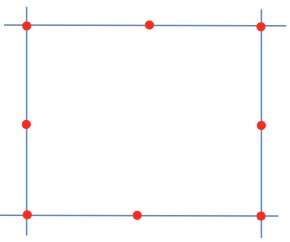I draw 4 three-in-a-line rows using 8 red points.
What is the smallest possible number of points to draw 4 three-in-a-line rows?
Inspired by a problem of Sam Loyd
Tricky Equation Puzzle: the equation below is wrong:
62 - 63 = 1
Which numeral has to be moved to make the equation correct?
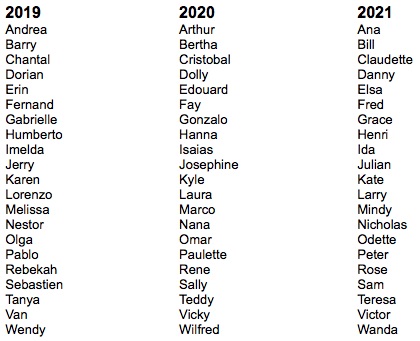Atlantic tropical storms are named through a strict procedure by an international committee of the World Meteorological Organization.
Based on the given table, guess how the tenth hurricane in 2023 might be named.
"300" costs $30;
"20" costs $20;
How much does "100" cost?
James was 16 years old last week, he will be 19 next year.
What is the date today?
It takes four minutes to boil an egg.
How long does it take to boil half of the eggs shown in the picture?
What total number of people can you be sure are not present in this scene?
You wish to make a table of all the prime factors of all the numbers between 1 and 1,000,000.
For example the number 12 would be written as 12 = 22 x 3.
and you would count 12 as having 3 (not necessarily unique) prime factors.
How many prime factors should you allow in your table?
by Leslie Green
Can you identify this creature?
Find the odd one out.
If we accept as fact that 80% of statistics are made up on the spot, what is the chance that at least one statistic out of the two unrelated statistics we have been given from independent sources is false (made-up)?
by Leslie Green
The term "per cent" is derived from the Latin per centum, meaning "by the hundred".
According to the Royal Statistical Society, 10% of the UK adult population does not understand percentages.
Which example confirms this?
Jim asks: "If John's son is my son's father, what relationship am I to John?"
When counting, what number is greater?
What is not sold in pairs there?
A clock fell to the ground.
What time is it?
Sheila Shelton sets sixteen sheep and six sheepdogs in a shed. How old is she?
This is a shop price tag written in French.
The tag says that BN Mini duo cereals are on sale for 3.95 instead of 3.15.
Is the rebate really 20% off?
Kitty has 222 marbles of different colors and the same weight except one, which is slightly heavier than any of the others.
You have a balancing scale with which you can compare the weight of the marbles by putting some in one pan and some in the other.
What is the minimum number of weightings you need to find which marble is the heavier one?
What is this collection of signs trying to tell you?
What is the smallest possible number of children in the boat, if John is among 3 heaviest and 2 lightest kids in the boat?
How many kids are there in the boat, if John is the second lightest and the third heaviest kid there?
Jane has rabbits, kittens, and chickens.
All of them are rabbits except three, all of them are kittens except four, and all of them are chickens except three.
How many chickens does she have?
Mary saw 5 crows walking on a newly seeded lawn.
John saw 4 crows walking there.
How many crows had walked on the lawn?
The picture shows a subway map.
A team of inspectors verifies passengers' tickets at a station on a line, or all lines through it if there are many lines.
Then they randomly choose the next neighboring station and move there to make their inspection.
At what station does Gerry have more chance of being inspected?
For the same volume, sand is twice as heavy as water.
Which is the heaviest?
Rock is ten times as heavy as wood.
Which is the heaviest?
How can you make the equation correct?
The International Air Transport Association (IATA) supports aviation with global standards for airline safety, security, efficiency and sustainability.
Each airport has an IATA three-letter code.
Which city's airport has the code LAX?
The sign on the bumper of a car reads CH.
What European country is it?
In what Olympic competition does the winner cross the finishing line facing backwards?
If the only brother of John's father's only sister has an only child, what would be relationship between the child and John?
A girl is facing a flat (planar) mirror in front of her.
What is the minimum possible height of the mirror in order for her to see herself entirely in the mirror?
How many rooms are there on the ninth floor of Math Jinni Hotel?
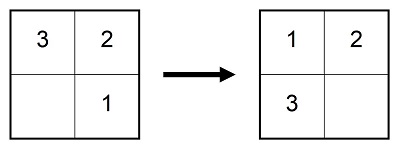The image shows a sliding square puzzle. Each square tile can move left/right/up/down if and only if the tile moves into the empty space.
How many moves are needed to go from the setup on the left to the setup on the right?
by Leslie Green
A typical problem for kids goes something like this:
"1 man digs 1 trench in 1 day. How many days would it take for 9 men to dig 2 trenches?"
This is a stupid question which an adult would not even bother with.
Why not?
(Pick the best answer)
by Leslie Green
In a family, each child has at least one brother and one sister.
What is the least possible number of children in the family?
What point does Gerry first need to target when striking the white ball in order to put it in pocket Z?
MENSA question.
What number can be added to the set below to complete it?
1, 2, 6, ?
I recently heard a riddle, and I wrote down what I heard.
"What can be black and white, but is red all over?"
MENSA question:
Which number goes next?
3, 3, 5, 4, 4, 3, 5, 5, 4,
There are two elves in front of an elf, two elves behind an elf and an elf in the middle.
How many elves are there?
Something is more useful when broken. Find an example.
What is the first letter of it?
Something gets wetter the more it dries.
What is the first letter of it?
Gerry said that the pin-code of his phone is the last four digits of the number π .
What is his pin-code?
Which proverb has a different meaning than the other three?
Never judge by appearances
Which of the following is closest in meaning?
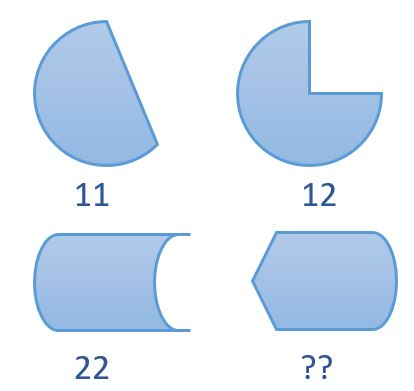MENSA question:
Using the first three shapes and values as a guide, find the value that corresponds to the last shape.
Leslie Green asks:
What is the secret message in the text below?
Mary Evans eventually took Michael, Ewan, and Tom Maudsley into Downton, not into Glasgow’s heavy traffic.
Jane's suitcase is the 8th suitcase in a line counting from the left.
Gerry's suitcase is the 7th suitcase in the line counting from the right.
There are 3 suitcases between them.
How many suitcases are there?
Logic Puzzle
Two fathers, two sons, and two doctors had a healthy breakfast.
Each person ate an apple.
What is the least possible number of apples that have been eaten?
One of the most ancient examples of literature on clay tablets says that Gilgamesh was 1/3 god and 2/3 human.
How many generations before his birth were the ancestors of Gilgamesh pure humans and gods?
If Gilgamesh existed, he probably was a king who reigned a kingdom in Mesopotamia sometime between 2800 and 2500 BC.
Leslie Green asks:
I have been told that I am six short of half a dozen eggs.
How many eggs do I have?
What came first, a chicken or an egg?
Mary's father has three kids. One is Alex. The second one is Beatrice.
Who is the third?
A claustrophobic gentleman chooses his place in the train that will enter a tunnel just after the station.
Where is the best place for him?
A dragon had a head in the morning. Every time a prince cuts off one head, three new heads emerge.
How many heads does the dragon have after seven heads were cut off?
Which shape should I use to form a square using four such pieces?
Which shape will not be used when I form a square using only four pieces?
What is the main reason that koalas sleep 18 - 20 hours per day?
The name KOALA derives from the ancient Aboriginal word meaning NO DRINK because these animals rarely drink water and receive most of their hydration from the water inside the eucalyptus leaves.
Which is certainly a fake coin?
Leslie Green asks:
It was announced on the UK news that birds were flying backwards in a certain location at a certain time.
Suggest the most plausible explanation for this report.
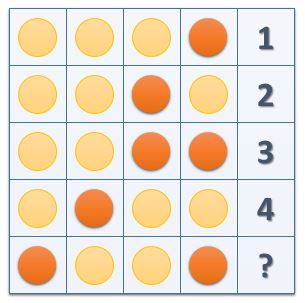Which number is missing?
How many different convex pentagons with the vertexes in 5 of these 8 points can be formed?
A convex polygon is a simple polygon (not self-intersecting) in which no line segment between two points on the boundary ever goes outside the polygon. For example, a regular hexagon is a convex polygon, while a star is not convex.
Jane said to Gerry 'If you give me two goldfish, then we will have an equal number of fish. If you give me one fish, then you will have double the number I have!'
What was the total number of fish they had?
Firefighters are taught to put on their pants in three seconds.
How many pairs of pants can a well-trained fireman put on in a minute?
What is correct?
If it were four hours earlier, it would be twice as long until midnight as it would be if it were four hours later.
What time is it now?
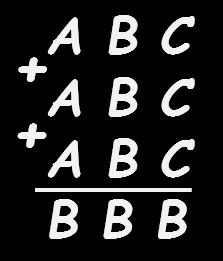If A, B, and C are different digits, what is their sum?
There are 12 words in the question below.
How many letters are there in the word which is spelt differently?
How many letters are there in the word which becomes shorter after adding two letters at the end?
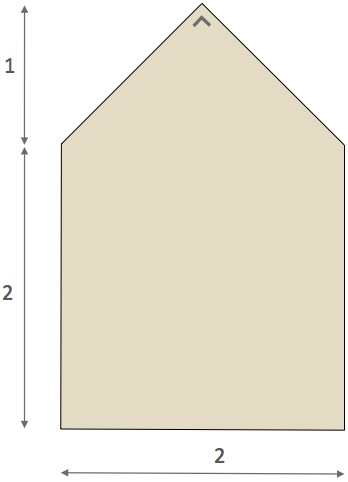A piece of wood is a square with a right-angled isosceles triangle on top.
A carpenter cuts it to form a square tabletop with no pieces left over.
What is the minimum number of saw cuts?
Source: Alex van den Branhof, Jan Guichelaar, Arnout Jaspers Half a Century of Pythagoras Magazine. MAA 2011
If certain words in this question are spelt wrong, how many of the eighteen words are spelt wrong?
You meet a boy from a region of two cities: Truth City and Lies City. Truth City dwellers always tell the truth, and Lies City dwellers always lie.
If you want to know the direction to Truth City at a fork of two roads what question will make him direct you correctly?
How many different ways are there to compose the word KAYAK, linking the circled letters by following the line segments in the picture?
Logic Puzzle
There are only X types of people:
those who understand binary and those who don't.
What number can replace X?
Logic Puzzle.
A European country has the highest ratio of men to women among its population in the world.
What is the first letter of the country name?
Logic Puzzle.
Many years ago a king of a North European country decided to establish which is more dangerous for health: tea or coffee.
He ordered that one prisoner should only be given coffee, and that another prisoner should only be given tea.
What do you think? Who died first?
Logic Puzzle.
A European country has the lowest birth rate in the world.
What is the first letter of the country name?
If it is raining at midnight in an old English town, what are the chances of the sun shining in 100 hours time?
How many eggs can the hens put in an empty basket?
Logic Riddle
In a family, each child has at least two brothers, three sisters, a father, a mother, three uncles and two aunts.
The picture shows only a part of the family.
What is the smallest possible number of people mentioned above?
Leslie Green asks
"Mary has a cat, and a rat, and a hat, and a mat.
If the cat is on the mat, and rat is in the hat, but the hat is on the mat, where is the rat?"
The discus throw men's Olympic record is 69.89 m and the women's Olympic record is 72.30 m.
Make a logical conclusion as to why the men's record is smaller than the women's record.
Which number has letters in alphabetical order?
Number SEVEN is mystic and frequently used in human culture.
What is the most reasonable cause of that fact?
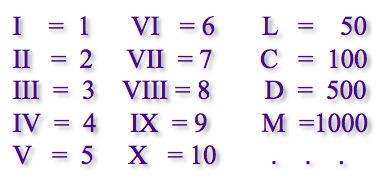Roman numerals are a numeral system of Ancient Rome based on letters of the alphabet.
For example, CVII is 107 (100 + 7).
What number cannot be represented in Roman numerals?
Kitty has 2017 marbles. The marbles are numbered from 1 to 2017. Marbles with equal digit sums have the same color.
How many different colors of marbles does Kitty have?
Logic puzzle.
What can you put into the eight empty boxes?
Logic puzzle.
If I remove one I get one more. What do I have at the beginning?
Leslie Green asks:
An American salesman flies over to London (UK) and for reasons best known to himself carelessly steps out of a first floor window. He breaks his leg.
Why?
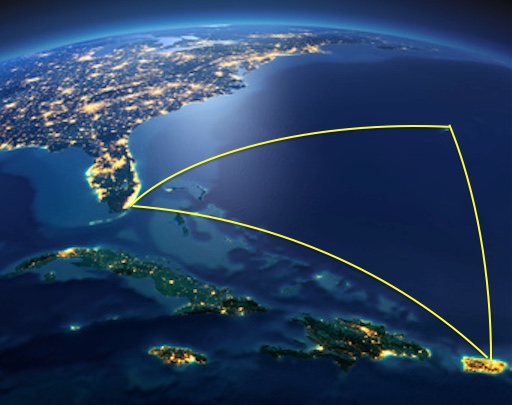What is the sum of the interior angles of the Bermuda triangle?
Barber paradox
In a city, the barber is the 'one who shaves all those, and those only, who do not shave themselves.'
Who shaves the barber?
A barber (from the Latin barba, 'beard') cuts, dresses, grooms, styles and shaves men's and boys' hair.
The picture shows a crescent.
What is the minimum number of lines needed to divide it into 6 parts?
A 99-people city chooses its mayor between Anna and Bill.
They have a strange rule: the first person chooses a candidate and the next two people always choose another one and so on. If the first person casts a ballot not marking anything at all, the next two people choose whatever they want.
What is the best strategy for Anna to win if she starts first?
I have a 5-litre bucket and two 3-litre buckets, all of which are half filled with water.
How much water is there in the buckets?
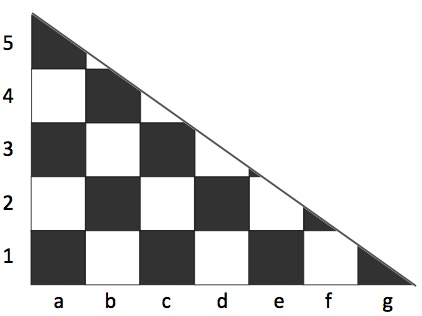This is a part of a chessboard.
What area is larger?
Choose a word that ends, includes and starts with letters E, N, D correspondingly.
What is the fewest number of splittings I would need to break the bar into 24 small pieces?
Each splitting consists of separating a single contiguous piece of chocolate along one of the grid lines.
I take off from Brussels, Belgium and fly 777 miles due south. Then, I turn the plane and fly 777 miles due west. I turn again and fly 777 miles due north, and finally turn and fly 777 miles due east.
Which country do I land in?
The first four Volumes of an Encyclopedia are stacked vertically side by side on a shelf. The thickness of a Volume is 10cm, and the thickness of the two covers of each Volume is 1cm.
What is the distance from the first page of Volume I to the final page of Volume IV?
A teacher explains to his students about taxes by eating 30% of their ice cream.
If each of 24 students has a cone of ice cream, estimate the amount of ice cream the teacher ate?
ONE + ONE =
You can add zero(s) where you want.
What can be the result?
A dog runs over a field.
He passes hens and cows.
He sees three times as many hens as cows.
Which of the following could be the total number of feet he saw?
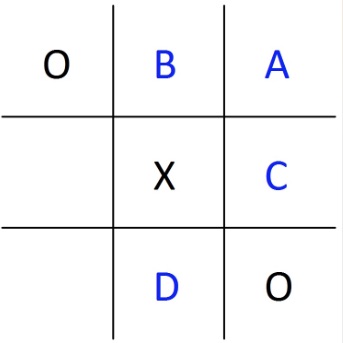In the game of noughts and crosses (tic-tac-toe) the winner is the player who gets three of their symbols in a straight line, with each player placing their symbol alternately.
In this game, noughts has started and it is now the turn of crosses to make their move.
Which move by crosses carelessly forces a win for noughts?
Author: Leslie Green
In how many ways can a wooden cube be cut into two congruent parts by a single straight line cut?
Brainteaser: A word becomes shorter when you add two letters to it.
How many letter are there in the word?
Alec, Beatrice, Crystal and Douglas opened their Christmas presents.
Alec opened 3 presents.
Beatrice opened 5 presents.
Crystal opened 12 presents.
How many presents were opened by Douglas?
Gerry picks up several coins from the pirate chest. All but 5 have an eagle. All but five are silver. All but 5 are at least 100 years old.
What is the minimum number of coins in his collection?
What is the main difference between the pictures on the left page and on the right page?
The problem is similar to 100 Bongard Problems on visual pattern recognition.
What is the main difference between the pictures on the left page and on the right page?
The problem is similar to 100 Bongard Problems on visual pattern recognition.
What is the main difference between the pictures on the left page and on the right page?
The problem is similar to 100 Bongard Problems on visual pattern recognition.
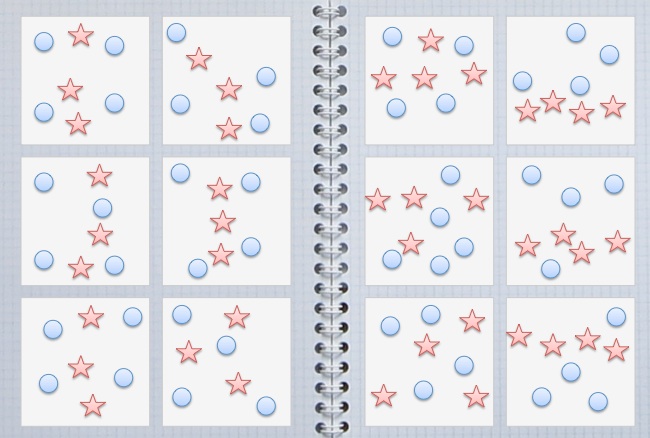What is the main difference between the pictures on the left page and on the right page?
The problem is similar to 100 Bongard Problems on visual pattern recognition.
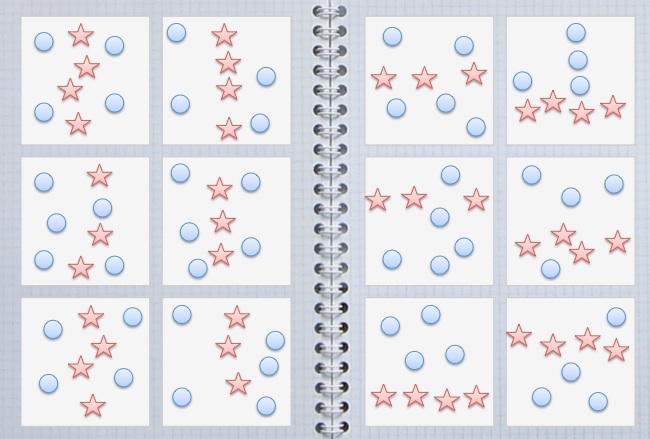What is the main difference between the pictures on the left page and on the right page?
The problem is similar to 100 Bongard Problems on visual pattern recognition.
M. Bongard (1924 – 1971) was a computer scientist. His tests played an important role in the disciplines of cognitive psychology and cognitive science.
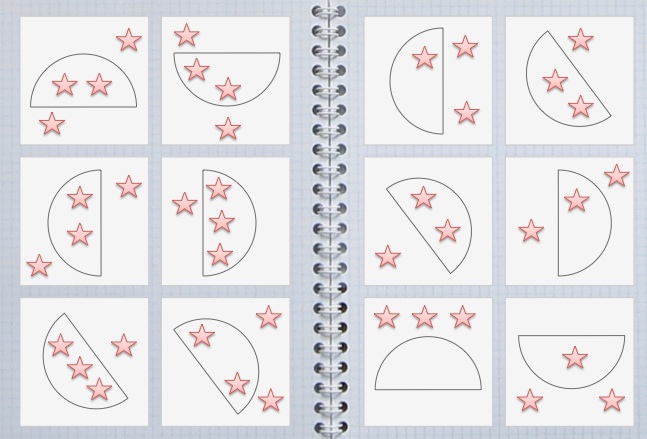What is the main difference between the pictures on the left page and on the right page?
The problem is similar to 100 Bongard Problems on visual pattern recognition.
There are only two handshakes in a meeting: John shakes hands with a person, this person shakes hands with Anna.
Does a man shake hands with a woman in the meeting?
What is the minimum number of matches that must be moved in order to obtain exactly two equilateral triangles (with no left over pieces)?
Anton, the highest IQ house ant on the planet, is taking his regular nocturnal walk from one corner of the chess board (1,1) to the diagonally opposite corner (8,8), moving only right or up the board at each successive square. He remembers that on square (5,3) there is a 'black-hole', so any valid route must exclude this square.
From how many different paths can he choose?
[HINT: You could try an easier problem first.]
Author: Leslie Green
THIS TEXT IS IN UPPER CASE.
This text is in lower case.
What is the difference between the number of letters in UPPER CASE and lower case in the text above?
What is the minimum number of matches that must be moved in order to obtain two equilateral triangles?
How many teeth does the Funny Man have?
If it rains at midnight in London, what are the chances that it will be sunny in 72 hours?
There are 2 matches.
What is the least number of matches that can be added to make 9?
I roll two dice, one with the left hand and one with the right.
If the left hand die gives an odd number, the overall score is zero.
If the right hand die gives an even number, I roll it again and again until it is odd.
The score is the sum of the two numbers, except for the previously mentioned case.
There are exactly 6 possible scores: 0, 3, 5, 7, 9, and 11.
What is the average score?
The problem was suggested by Leslie Green
I add blue blocks one by one on the top.
Does the structure fail?
In a room, there are 3 bosses, 2 wives, and a plumber.
What is the least possible number of people in there?
A short word can be written forward, backward or upside down while remaining the same word.
What is the first letter of the word?
You have more shoes than an average child in your country.
This statement is . . .
Solve this.
F = (a - x) (b - x) (c - x) . . . (z - x)
What letter goes next?
A E F H I K L M N
The calculation is correct.
Which number is hidden by the clouds?
What is missing?
If
One, Nine, and Eight gives ONE
what is
Two, Eight, and Nine ?
If today is the payday in Bob’s company, what happens in two days?
What is missing?
Kate was born on December 31st, yet her birthday always falls in the summer.
Where does she live?
A shopkeeper of a Dairy stands six feet tall and wears size 13 sneakers.
What does he weigh?
A brick weighs 5 pounds and half a brick.
What does a brick and a half weigh?
If you take one third of GOOGLE and two thirds of ATT, what do you get?
What is half of work and one third of gentleman?
Two American coins add up to 35 cents but one of them is not a dime.
What is the coin?
Penny = 1 cent.
Nickel = 5 cents.
Dime = 10 cents.
Quarter = 25 cents.
If you were to spell out the numbers, how far would you have to go before encountering the letter 'a'?
Crazy Logic. Choose a number.
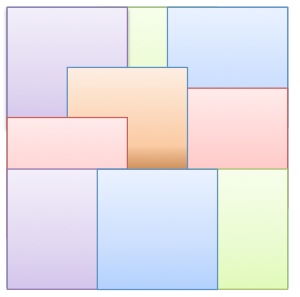An arrangement is formed by laying nine colored squares of the same size one over another.
Which square is laid at the bottom?
What triomino goes next?
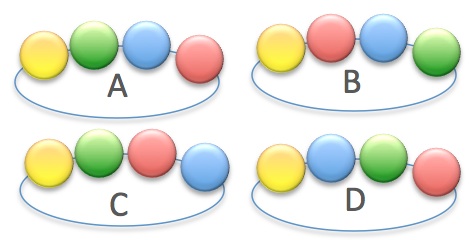Jane wants to make different bracelets.
Which bracelets are the same?
Find the odd one out.
In a room, there are 3 bosses, 2 wives, and a plumber who works for the government.
What is the least possible number of people in there?
What is the smallest integer that can be written with two digits?
Which goes next?
N NE E SE S
How long is a rope that is 8 meters shorter than another rope that is 5 times the length of the first rope?
John is Jim's son.
Jay is John's son.
John is a doctor's son.
His father is not a doctor.
Who is the doctor?
Three U.S. coins add up to $1.
If one of them is not a half dollar, what is the smallest-value coin?
If you make one word using each letter below only once, what place does the letter e take?
e r t s s s
Gerry gave half of his money to Jane.
Next day, she gave half of all her wealth to Gerry.
After the last exchange they each have exactly as much as they originally started with.
Who is richer?
How many letters are there in the word that all smart students spell incorrectly?
Which of the following is least like the others?
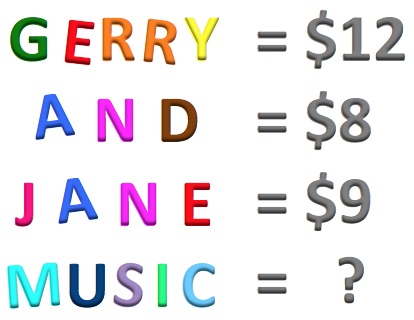Guess!
What is the word coiled inside this circle?
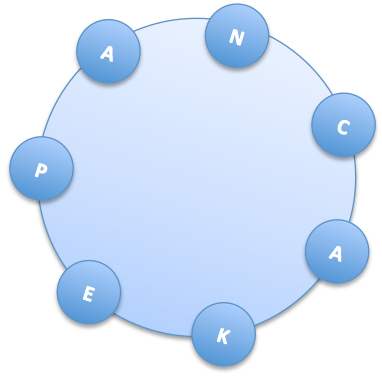What is the word coiled inside this circle?
For which shape did I use more wood?
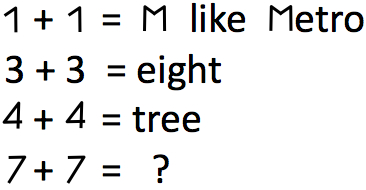Guess!
Which regular shape cannot be used to tile a floor with no gaps between tiles?
What is the maximum number of sections into which a pancake may be divided by four straight cuts through it?
(NOTE: The pieces cannot be re-arranged between cuts.)
Gerry's circular garden is 1200 m in diameter and has no fence.
How far can a wolf run into the garden?
Which is correct?
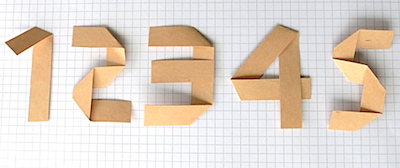Which number required the most paper?
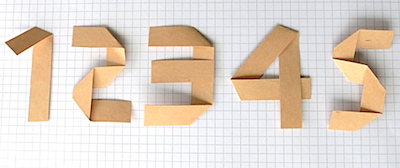I composed the numbers from strips of paper.
Find the odd one out.
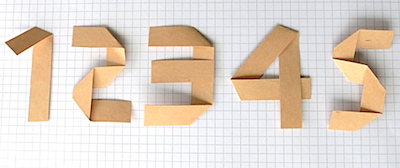I composed the numbers from strips of paper.
Find the odd one out.
If each coconut is priced at $9, then the shopkeeper loses $11.
If each coconut is priced at $11, then the shopkeeper gains a profit of $9.
How many coconuts are there?
How many pentagons are there?
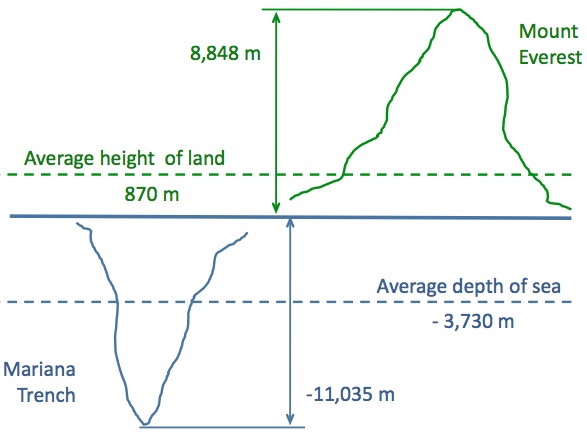The diagram shows the lowest point and the highest point of our planet.
What place is the closer for John who lives in London?
Source: Nelson Thornes New Maths in Action. 2004
"This is a capital letter of the alphabet that's been folded just once.
Which letter is it if I unfold it? "
The puzzle was created by puzzlemaster Scott Kim
Once upon a time, there were three little pigs - ages 2, 4, and 6 months.
If one was born in January, when was one of his brothers born?
Which is a better fit?
The smaller the percentage of the ‘area left over,’ the better the fit.
There are 5 children in a boat.
Four of them do one of the activities below.
What is the fifth kid doing?
I have 33 coins.
What is the minimum number of coins I need in order to make sure that each coin touches exactly three other coins?
A pirate boat is floating on a lake.
The pirates throw a heavy chest with gold coins overboard.
What happens with the water in the lake with respect to the shore?
The amount of water flowing into a tank doubles every minute.
The tank is full in an hour.
When was the tank a quarter full?
You have 3 coins.
One is counterfeit and is either heavier or lighter than the other two.
How many moves are needed with a balance beam scale to isolate the counterfeit coin?
There is an equal number of boys and girls.
Share $10 among them so that each girl gets $1 more than each boy.
How much does each girl get?
How many uninteresting numbers exist?
The question is based on the interesting number paradox, which is a semi-humorous paradox, which arises from the attempt to classify natural numbers as "interesting" or "dull."
You pay $6 to enter a game.
You roll 2 dice.
You then have two choices: you can cash out and get paid the dollar amount of the roll, or you can pay $1 to roll the dice again.
What is your final gain per game if you play many times and choose the strategy to stop once you get more than 6 on two dice?
One by one, 40 cars enter a company parking lot with 40 assigned places.
The first driver forgets his place number and takes a random place.
The remaining drivers take their assigned place, if available, or take a random place.
What’s the probability that the last driver ends up in his original assigned place?
Inspired by Peter Winkler's airplane problem.
One quarter of the competitors were faster than Mary and I, but two thirds were slower.
How many people were swimming?
Find the logic:
12345678 → 4
234567 → 2
3456 → 2
45 → X
Find X.
Management support accelerates the execution of a project by 10% during the first year of the project.
The same support delays the project execution by 10% during the second year.
Will the project execution take more or less time with management support?
Mary and John manage two different projects and they have a common budget.
Mary spent half of the budget, then John spent half of what was left, then Mary spent half of what was left and so on until the last cent.
What proportion of the budget did Mary spend?
John and I have a glass of milk.
He drinks half of it and then I drink half of what is left.
He drinks half of what is left and I do the same.
We continue until nothing is left.
What proportion of the initial amount of the milk did I drink in total?
A father has left 47 donkeys for you to distribute to his three sons;
1/2 (23.5) should go to his eldest son,
1/3 (15.667) to the middle one, and
1/8 (5.875) to the youngest.
You arrive with your own donkeys.
You can add or take some donkeys from the herd.
How do you divide them so that all sons are happy with your decision?
How many donkeys does the eldest son get?
Inspired by Malba Tahan “The man who counted.”
If you were to spell out the numbers, how far would you have to go before encountering the letter 'g'?
The wind in the open-air swimming pool increases the westward swimming speed and decreases the eastward swimming speed by 1 mile per hour.
Will this swim take more or less time than the swim without the wind?
How many "yes or no" questions are needed to guess any 3-digit lock code?
How many "yes or no" questions are needed to guess any 5-digit code?
In a city, sixty percent of the men are married to eighty percent of the women.
Estimate the percentage of the married adults in the city.
Which symbol goes next?
If regular stars are placed as shown to form a complete circle, how many stars are needed?
Job interview logic puzzle in a bank.
Which of these pieces of information would be most useful for estimating the number of people who travel in a train with 20 passenger coaches?
Thinking outside the box.
Solve this:
A doctor gave me 7 pills and told me to take one every half hour.
How long would they last?
Anna has 8 biscuits, Bill has 6, and Cindy has 1. They share them out equally. Cindy pays for her biscuits by leaving 8 wafers.
What is the fairest way for Anna and Bill to share out their wafers?
Thinking outside the box:
Which statement is correct?
I multiply the two page numbers and get 6162.
What is the right-hand page number?
Engineers at a race company make three discoveries.
The first invention saves 50% of fuel, the second 30%, and the third 20%.
If the company uses all three innovations at once, how much fuel does a car consume compared with a normal car?
If you rearrange the letters NAPDOL, you would have the name of a
Mount Everest is the Earth's highest mountain with a peak at 8,848 meters (29,029 ft) above sea level.
Indian mathematician Radhanath Sikdar was the first to identify Everest as the world's highest peak in 1852. Edmund Hillary and Tenzing Norgay reached the summit on 29 May 1953.
What was the highest mountain in the world before Mount Everest was discovered?
Can you predict the score of any match before it begins?
What is the score of England against France tomorrow?
United we stand, divided we fall.
How many sets of antonyms are there in the saying?
Logic puzzle.
A word for a family member is the same spelled forward and backwards.
How many letters does the word have?
How many months have 30 days?
Find the missing part.
Is it legal for a man in Montana to dance with his widow's sister at her marriage ceremony?
What word has letters that are not in alphabetical order?
Which is the odd one out?
Which city is the odd one out?
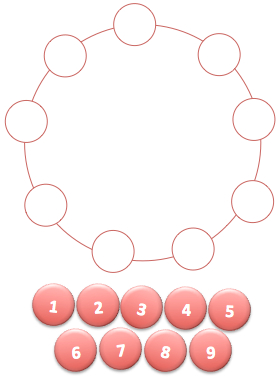Arrange nine numbers in a circle so that the difference between neighboring numbers is always less than 3.
Which of the following pairs cannot be neighbors?
What is half of 8?
A four-letter word can be written forward, backward or upside down while remaining the same word.
What is the first letter of the word?
After a three-hour drive, I stopped my car in front of a wall with three doors: a silver door on the left, a gold door in the middle, and an iron door on the right. Which door would I open first?
"Letter frequency. Accurate average letter frequencies can only be gleaned by analyzing a large amount of representative text." (source: Wikipedia)
What is the most common letter in the English alphabet?
There is only one correct answer to the question below.
Which answer is correct?
Which direction is the London coach going?
The Babylonians used a base 60 number system.
What shape inspired them to decide that a circle has 360 degrees?
The five pieces of chain shown must be joined into a long chain.
How many rings should be opened and closed?
Inspired by Boris Kordemsky
Logic riddle:
In a house, there are three switches on the ground floor and a light bulb in the cellar. I cannot see the light from the ground floor.
What is the minimum number of trips to the cellar I need to make to identify which switch corresponds to the light bulb?
We assume that the bulb in the cellar works, that there is power to the house, and that one of these three switches will switch on the cellar light.
A surgeon has two pairs of surgical gloves.
What is the maximum number of people on which he is able to operate?
NOTE:
1)There is no blood contact between the people including the surgeon.
2) The surgeon needs to use both hands for each operation.
Adding a letter to a word makes it odd.
What is the word?
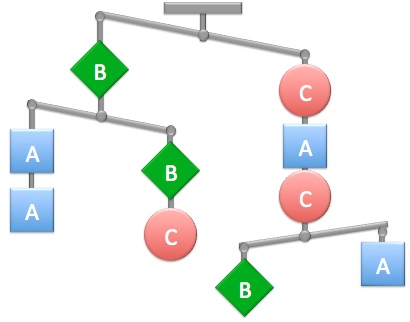Order the shape by weight from lightest to heaviest.
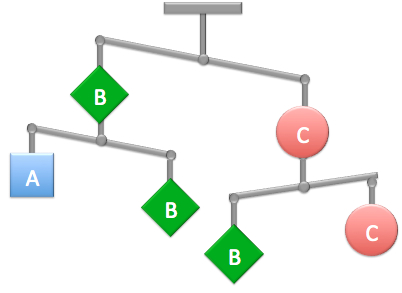Order the shape by weight from lightest to heaviest.
How many coins must you move to form two infinite lines, each with exactly five coins?
If 2 salesmen can sell three luxury cars in 4 days, how many luxury cars can five salesmen sell to six clients in 7 days?
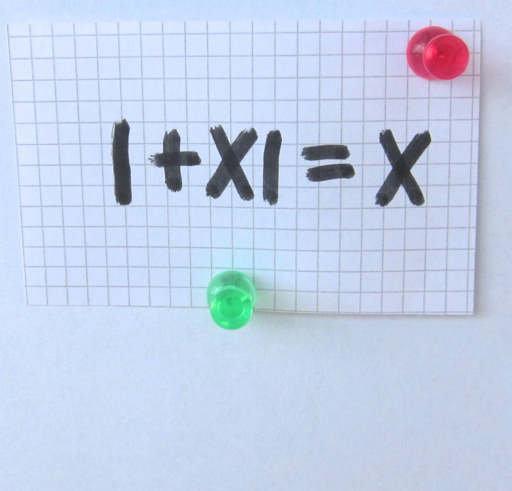Logic question.
What is the easiest way to make the following equation correct?
If I delete a letter in a word, then only one is left.
Find the word.
The figure shows a triangle made of discs.
I want to move two discs and turn the triangle upside down.
How many different ways can I do this if a disc moves less than its three-diameter distance?
What is the letter, which goes before O?
Find the odd one out.
Logic puzzle: a secret door.
A man approached the door of a secret laboratory and the door robot said "SIX." The man replied, "THREE" and was let in.
Another day, the robot said, "TWELVE."
The man replied, "SIX" and was let in.
Today, the robot said, "TWENTY."
What should the man say?
Four starfish have 20 arms.
How many starfish have 35 arms?
Anna ran in the north direction at a speed of 3 miles per hour, Bobby ran west at a speed of 4 miles per hour, and their dog, Rex, was running between them at a speed of 9 miles per hour.
What was the distance between the children in one hour?
Tricky Equation Puzzle: the equation below is wrong:
12 + 3 = 4
Which numeral has to be moved to make the equation correct?
Which of these parts has the largest area?
It costs $24 to paint a cube.
Before painting, it was cut in four pieces by two planes.
What is maximum possible cost to paint these four pieces?
The blocks of ice are of the same height.
Which assembly melts slowest?
The total weight of Bob and his sister Anna is 151 kilograms. Bob's weight is 1 kilogram more than twice Anna's weight.
What is Anna's weight?
For which letter did I use the greatest amount of green paint?
Brad has as many brothers as sisters.
What is the largest number?
The number of hours left today is a third of the number of hours already passed.
What time is it?
One word on this page is spelt incorrectly.
How many letters are there in the word?
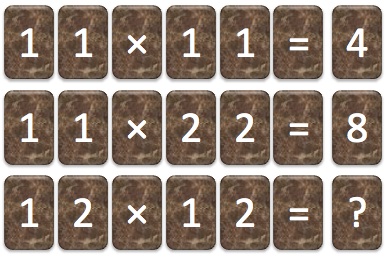What is the logic behind?
What is the correct answer?
How many apples can I place, such that the distance from every apple to every other apple is a single fixed value?
John is 33 years, 33 months, 33 weeks, 33 days, and 33 hours old.
How old is he?
Logic puzzle:
What happens once in a minute, twice in a week, and once in a year?
Logic puzzle:
Counting down from 100 by one, which number comes next?
It takes exactly 1 hour to burn a rope when I light one of its ends.
The rate of burning is completely random, but the final result is always 1 hour.
How many different periods of time can I measure with 2 such ropes?
A magician placed 3 bowls of fruit in 3 closed boxes and 10 people tried to guess which fruit was in which box.
One person guessed all 3 fruits correctly, 3 people guessed only 1 fruit correctly.
How many people did not guess any fruit correctly?
A donkey must transport 900 carrots to the market, which is 300 miles away.
The donkey carries a maximum of 300 carrots, and eats 1 carrot every mile.
What is the largest number of carrots that can be delivered at the market?
I have a rectangular piece of cheese with a round hole.
What line cuts the piece of cheese into two parts of equal weight?
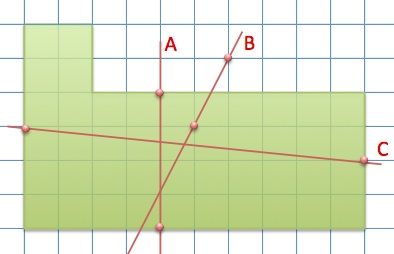What line divides the green polygon into two parts of equal area?
What is the largeest number of matchsticks I need to remove to make 10?
What is the next letter in this series?
On average there are 100,000 strands of hair on a person's head.
Hair grows at a rate of about 15cm a year and each hair lasts up to 6 years before it falls out.
If the population of London is 8,000,000, what is the probability that at least 2 of the inhabitants have the same number of hairs on their heads, discounting bald people?
Find the odd one out.
Logic riddle
This occurs once in every second, once in every hour, and twice in every afternoon.
How often does it occur in every month?
Logic riddle
In a house, there are three switches on the ground floor for three light bulbs in the cellar. I cannot see the lights from the ground floor.
What is the minimum number of trips to the cellar I need to make to identify which switch corresponds to which light bulb?
Bill (B), Cindy (C), and Daniel (D) work on a project.
(1) Together, B and C can complete it in 10 days.
(2) Together, C and D can complete it in 12 days.
(3) Together, D and B can complete it in 15 days.
How many days are needed for Bill to complete the project on his own?
Find the angle between two diagonals drawn on two faces of the cube.
Logic puzzle: a secret door.
A man approached the door of a secret laboratory and the door robot said "SIX." The man replied, "THREE" and was let in.
Another day, the robot said, "TWELVE."
The man replied, "SIX" and was let in.
Today, the robot said, "FOURTEEN."
What should the man say?
You have 240 golden bricks identical in size and appearance but one is lighter than the others.
How many times do you use a balance scale to find the odd brick?
I arranged eight wooden sticks in the shape of a fish.
What is the minimum number of sticks that must be moved to make the fish face another direction?
I want to measure exactly six minutes from the moment I touch an hourglass, using only a five-minute hourglass and a four-minute hourglass.
How many times do I flip over an hourglass?
Count the initial flip(s) and find the minimum possible number.
Find a phrase that differs from the others.
There is a legend that a stork brings babies to a village.
All parents continue to have children until they have a boy.
If they have a girl, then they try to have another child.
They stop if they have a boy.
The probability of giving birth to a boy is 50%.
What is the proportion of boys to girls in the vilage?
The photograph courtesy of Roland Sauter
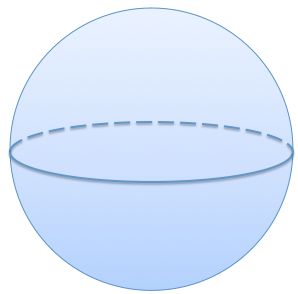What is the maximum number of apples (ideal spherical units) that can touch another given apple (spherical unit) without overlapping?
Guesstimation.
How many tennis balls can fit in a school bus?
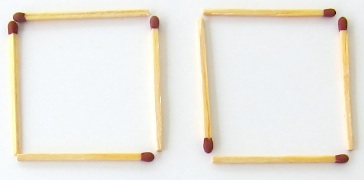Four matchsticks form a square.
How many non-overlapping squares can be formed using eight matchsticks?
Note: The matchsticks do not intersect each other.
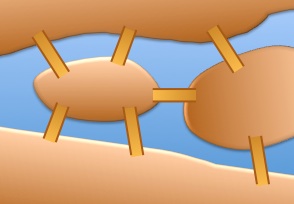In a city, there were seven bridges.
There was a tradition to walk and cross over each of the seven bridges.
If a person starts and finishes at the same point, what is the smallest number of crossings the person would have to make?
Anna (A), Bill (B), Cindy (C), and Daniel (D) work on a project.
(1) Together, A, B, and C can complete it in 10 days.
(2) Together, B, C, and D can complete it in 11 days.
(3) Together, C, D, and A can complete it in 12 days.
(4) Together, D, A, and B can complete it in 13 days.
Who is the best performer?
Large individual letters are differently priced.
The letters in the word SPRING cost $19.
The letters in the word SUMMER cost $20.
The letters in the word AUTUMN cost $21.
The letters in the word WINTER cost $20.
How much would the letters in the word SEASONS cost?
There is insufficient information to solve this problem.
Use the simplest assumption which exactly matches one of the answers given below.
In a city, there were seven bridges.
There was a tradition that a newly married couple walks and crosses over each of the seven bridges only once.
If a couple starts and finishes at the same point, which city plan allows the couple to acomplish this task?
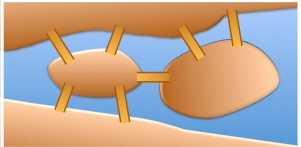In the city of Konigsberg there were seven bridges.
There was a tradition to walk and cross over each of the seven bridges.
If a young man starts and finishes at the same point, what is the smallest number of crossings he would have to make?
The Legend of Carthage: Queen Dido and her followers arrived in North Africa.
The locals told them that they could have the coastal area that an ox hide would cover.
She cut the hide into a series of thin strips, joined them together, and formed a coastal shape.
The ox-hide enclosed area was known as Carthage.
If you had a 10 km long strip, which shape (rectangle, triangle, semi-circle, or semi-ellipse) would you choose to maximize the enclosed area?
Find the best deal.
Thinking outside the box:
52 - 28 = 4
Which digit has to be moved to make the equation correct?
Three apples were weighed in pairs and the weights were 200, 204, and 208 grams.
What is the weight of the lightest apple?
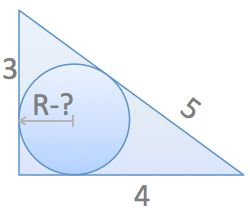Find the radius of the circle.
What would this picture look like in a rearview mirror?
In a family photo, I see 1 grandmother, 1 grandfather, 2 fathers, 2 mothers, 2 daughters, and 2 grandchildren.
What is the smallest number of people possible that are in the family photo?
I arrange 10 points so that 3 lines each go through 4 points.
I would like to rearrange these 10 points.
What is the greatest number of lines that go through 4 dots each?
What is the maximum number of pieces that an apple can be divided into with four straight planar cuts?
The pieces do not move.
A bee crawls along the sides of the honeycomb hexagons.
It has moved from point A to point B along the shortest possible path.
It can move in three different directions and made an even number of steps.
What statement is correct?
Find the next letter in the sequence.
Bob the plumber has 10 pockets and 60 nuts.
He wants to put the nuts in all of his pockets so that no two pockets have the same number of nuts.
What is the largest number of nuts that a pocket can possess?
Which shape must be placed in the empty space?
If each row and each column of the square must contain exactly one triangle, circle, pentagon, and rhombus, which shape must be placed in the empty white cell?
I want to move just one matchstick to make the phrase correct.
From which part will I take the matchstick?
Which matchstick do you remove to make the equation correct?
I would like to cut the shape into the fewest possible pieces that will fit together and form a rectangle.
What is the smallest number of pieces?
Three boys want to equally share three pancakes.
The picture shows the pancakes' diameters.
Which part of the largest pancake will one of the boys receive?
How many circles are needed to separate each star from all of the others?
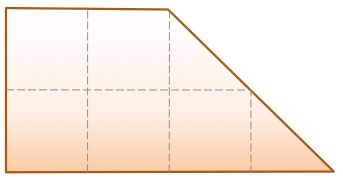I want to cut this shape into four pieces all of precisely the same size and shape.
Which is such a piece?
Each child in a family has at least one brother, two sisters, and two parents.
What is the fewest number of children their parents might have?
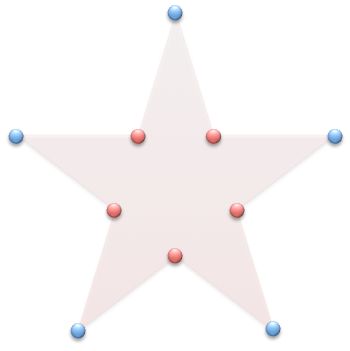How many different lines that extend to infinity in both directions can you draw through any two of these ten points?
For which letter did I use the greatest amount of green paint?
Anna ran in the north direction at a speed of 8 km/h, Bobby ran east at a speed of 14 km/h, and their dog, Rex, was running between them at a speed of 20 km/h.
How far did the dog travel in one hour?
Tricky Equation Puzzle: the equation below is wrong:
102 - 99 = 1
Which numeral has to be moved to make the equation correct?
Logic puzzle.
There are three mothers and three daughters in a group of people.
Each mother has a daughter in the group.
What is the smallest possible number of people in the group?
How many times do the two hands of a clock point in the same direction between 9:00 am and 9:00 pm ?
Benny Bunny starts jumping from a hole.
Every leap is two times longer than the previous one.
Does Benny have a chance to come back to the hole?
How many times higher than the tree is the rainbow?
A banker forgets which key fits in which of three keyholes.
What is the minimum number of trials to identify which key is meant for each lock?
Which pair of shapes is not like the others?
Enclosed is a lamb using a 4-crosspiece log fence.
What is the smallest number of crosspieces I needed to separately enclose four lambs?
There are 10 girls and 10 boys in a class.
A teacher randomly chooses two students.
What is the probability that they are a boy and a girl?
Which spring wire is longest?
Four matchsticks form a square.
How many non-overlapping squares can be formed using seven matchsticks?
The matchsticks make four small squares and one big square.
How many matchsticks do I need to remove so that there are no squares in the picture?
Find the minimum number.
A girl wants to cut the paper into several equal pieces of the same shape, and with nothing left over.
(NOTE: She does not have to cut along the dotted lines.)
How many pieces are possible?
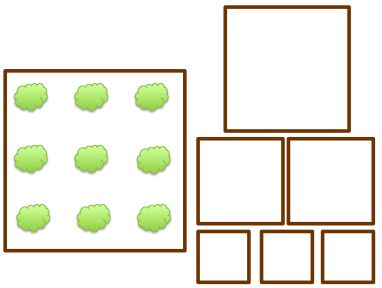I enclosed 9 apple trees using a large square fence.
What is the smallest number of square fences I need to add in order to separate all the trees?
There are eight buckets; four of them are filled with water.
What is the smallest number of buckets that I can move to make the pattern: full bucket, empty bucket, full bucket, empty bucket, etc.?
I want to cut round bread into eight equal pieces.
What is the smallest number of straight cuts I can make to achieve this?
Estimate the number of flags in the picture.
This shape was formed by removing a small cube from a big cube.
The volume of the removed cube is 1/4 of the big cube's volume.
Find the surface area of the shape compared with the surface area of the big cube.
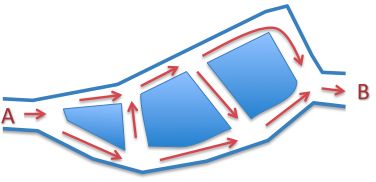How many different ways are there to go from A to B?
Which of these diagrams could be drawn completely without lifting the pen off the paper or going over any line twice?
What is the lowest number of chain links that must be opened and closed to join the pieces shown on the right into a circular chain?
How many fish DO NOT swim to the left?
Which of these diagrams could be drawn without taking the pen off the page and without drawing along a line twice?
Which of these diagrams could be drawn without taking the pen off the page and without drawing along a line twice?
Which shape fits in the missing space to complete the pattern?
Find the missing figure.
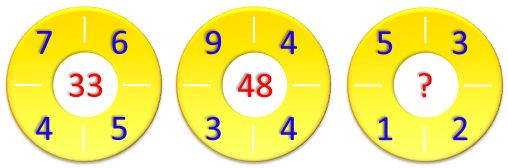What number should replace the question mark?
What number should replace the question mark?
What do the snowflakes have in common?
Which of these parts has the smallest area?
What is the lowest number of chain links that must be opened to join the pieces on the right into a circular chain?
How many squares can be formed by joining four of these points on the rectangular grid?
I fold a square piece of paper in half four times without unfolding, making an isosceles right triangle each time.
What is the correct net of the creases on the paper after unfolding the paper?
Each child in a family has at least 3 brothers and 4 sisters.
What is the smallest number of children their parents might have?
A lady, attempting to avoid revealing her real age to her husband, says:
I'm twenty-two years old if you do not count weekends and one summer month of every year.
Guess her real age.
The product of 2 integers is 1000.
Find the smallest possible sum of these numbers.
The blocks of ice are of the same height and depth.
Which assembly melts fastest?
Choose the bolt head design that can be easily turned with the household wrench.
Twenty matchsticks form five squares (one 3x3 and four 1x1).
How many matchsticks do I need to move to make seven squares?
Find the minimum number.
You have eight dimes; seven are real and one is fake.
All the real ones weigh the same, and the fake weighs less than the real ones.
How many times do you use a balance scale to find the fake dime?
What is the largest number you can write with just two different digits?
Five students put their sandwiches into five paper bags.
The bags are randomly distributed to the students.
What is the probability that exactly 4 students receive the correct bag?
The figure shows a triangle made of discs.
I want to move the discs and turn the triangle upside down.
What is the lowest possible number of moves that I must make?
The matchsticks make a spiral that goes clockwise.
How many matchsticks do I need to move to make the spiral go counterclockwise?
Find the minimum number.
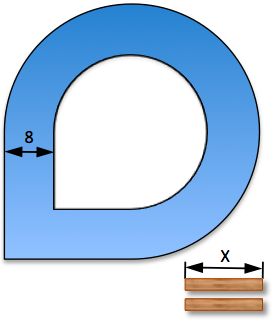A gardener has to reach the island in the middle of a pond without getting wet.
The gardener has two planks each X feet long.
What is the smallest length of the planks?
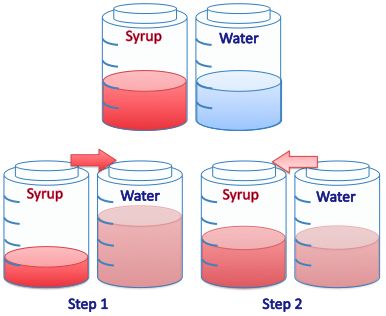You take half of the syrup and mix it with the water, and then take the same quantity from the water jar and mix it with the syrup.
Does the syrup now contain more water than the water does syrup, or the other way round?
1. At least 1 of these 6 statements is false
2. At least 2 of these 6 statements are false
3. At least 3 of these 6 statements are false
4. At least 4 of these 6 statements are false
5. At least 5 of these 6 statements are false
6. At least 6 of these 6 statements are false
How many sentences are true?
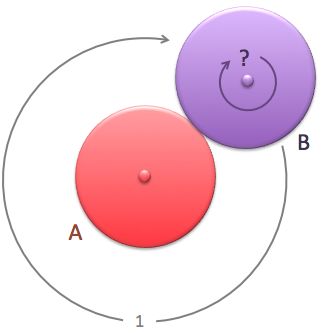There are 2 identical circles. Circle A remains fixed, while Circle B makes 1 turn around the first one, touching it without slipping.
How many turns has Circle B made around its own axis?
How many straight lines are needed to separate each star from all the others?
If 9 workers can build 9 houses in 9 months,
then how many months would it take 11 workers to build 11 houses?
The twins are the same height.
They place four identical blocks as shown in the figure.
How tall are the boys?
A father wishes to divide a square piece of land among his five sons.
He gives one quarter of the land to the first son, as shown.
He divides the remaining land into four plots of equal size and shape.
Find the plot.
Source: James F Fixx, Solve It!, 1978
How many boxes measuring 0.1m x 0.1m x 6.8m can be packed into a container measuring 6m x 3m x 2m?
How many planes of symmetry does a cube have?
A boy cuts a cardboard circle and only cuts 5 straight lines.
He does not care if the pieces are equal.
What is the maximum number of pieces he can obtain if he makes 5 cuts without moving the cut pieces?
How many times do the hour and the minute hands form a 90-degree angle in the course of 12 hours?
How many planes of symmetry does a brick have?
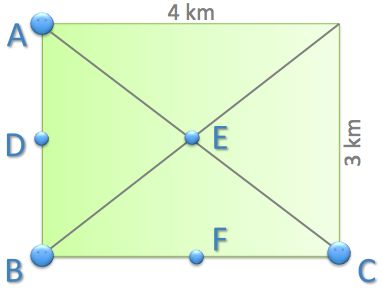Three referees A, B and C are at the corners of a rectangular field.
At which point should the referees meet so that the time they walk to that point is minimized?
Is the number of people in the world that has shaken hands with an odd number of people odd or even?
Source: Fixx, James F. - Solve It!, 1978
How many planes of symmetry does an Egyptian pyramid have?
How many generations forward must you go in order to have more than one thousand ancestors?
A wheel with a red mark on it is rolled along a straight line.
What is the path the mark follows during one revolution?
Alex needs six tacks to fix two rectangular pictures because he can overlap the pictures.
What is the least number of tacks he needs to tack eleven pictures?
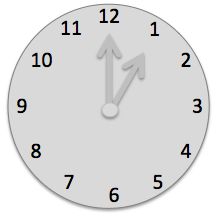Which statement is NOT correct?
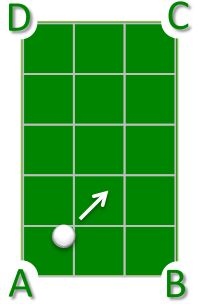I strike a pool ball from corner A of the rectangular billiard table at an angle of 45°.
Into which corner pocket will the ball fall?
Eugenia, the magician, receives a 50% discount every time she asks for the price.
She bought a $100 puppy for less than $1.
How many times did she ask for the price?
Three boys, A, B, and C, are at the corners of a rectangular field.
At which point should the boys meet so that the sum of the distances they walk to that point is minimized?
Ten men met at a conference.
Each man shook hands with each of the other men exactly once.
How many handshakes took place?
The total weight of Bob and his sister Anna is 155 kilograms. Bob's weight is 2 kilograms more than twice Anna's weight.
What is Anna's weight?
For which letter did I use the smallest amount of green paint?
Brad has as many brothers as sisters.
How many more brothers than sisters does his sister Sue have?
There are 20 students in a class. 12 students have red stars and 8 students have green crosses; 6 students have nothing.
How many students have both?
The number of hours left today is half of the number of hours already passed.
What time is it?
Christmas week has a Wednesday in it.
This statement is . . .
A sculptor cut a corner of a cube.
How many faces does the new shape have?
How many of the letters in the Russian alphabet have more than one line of symmetry?
How many letters are there in the correct answer to this question?
Each of four children has a photo.
Anna and Bill's photos show water.
Only Cindy and Bill's photos show a man.
Which photograph belongs to David?
Mrs. Johnson is placing apples on shelves, as shown here.
Estimate the total number of apples she can fit on the two shelves.
How many stars will be in the fourth line of the pattern?
Coding Puzzle 
There is an error in the sign on a street during an infection. 
Find two numbers that are added up to another number in the picture.
Which two roads look the same in the picture?
Move just one card to make the equality correct. 
Find the missing number.
Gerry encoded a message for Jane. 
Jane encoded a message for Gerry. 
What is the maximum number of pieces a doughnut can be cut into by 3 straight cuts? 
Which number is decreased by 12 if you turn a piece of paper on which it is written upside down?
Brain Teaser 
Which number goes next? 
What can be even bigger than an elephant, but weighs nothing?